These tables of values represent continuous functions. In which table do the values represent an exponential function?

continuous functions:

a function is said to be continuous , if it is an increasing function or decreasing function or both increasing and decreasing function.

if function is increasing continuous function

then for, [tex]x_{1}> x_{2}, then , f(x_{1}) > f(x_{2})[/tex]

if function is decreasing continuous function

then for, [tex]x_{1}> x_{2}, then , f(x_{1}) < f(x_{2})[/tex]

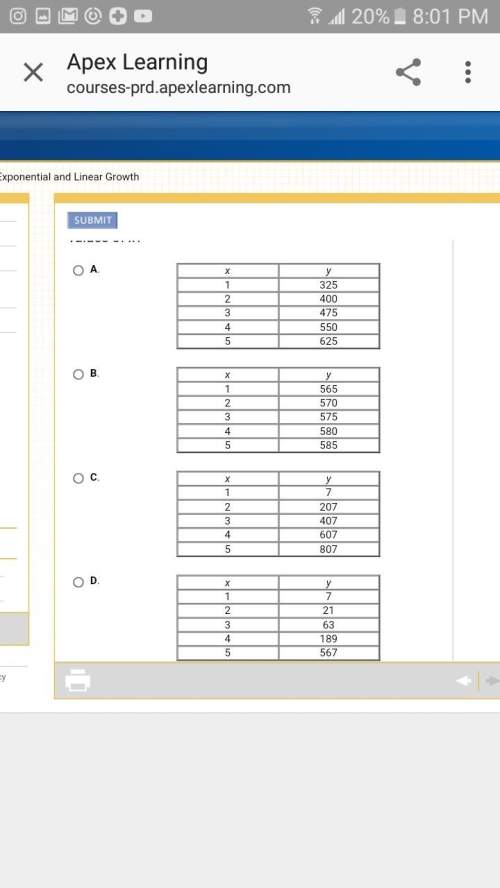
so , in the situation described,for which functions will the y-values be the greatest for every large values of x describes continuous increasing function.as i have defined continuous increasing function

the function having larger slope, will have larger y values , for larger values of   x .

slope between two points (a,b) and (p,q) is given by :

m=[tex]\frac{b-q}{a-p}[/tex]

slope in option 1 =75

slope in option 2 =5

slope in option 3 = 200

as the fourth option is a geometric progression, common ratio being 3. as x value increases by 1 , y value increases 3 times.the function can be written as: y=7.[tex]3^n[/tex] [n=0,1,2,3]

option (3) and option (4) is right choice.in each case y value increases with increase in value of x.

I would have to go with chart B

Step-by-step explanation:

It is demonstrating exponential growth, by the factor of 100,

exponential growth is when the number increases by a drastic amount.

I hope this helped you and anyone else who may come across this.

I belive its A

Step-by-step explanation:

The table D represents the function that will have the greatest y-values for very large values of x.

Step-by-step explanation:

The table A represents a linear function, for which each one unit increment in the "x" variable produces a three unit increment in the "y" variable. This means that the growth rate of this function is 3.

The table B also represents a linear function, for which each one unit increment in the x variable produces a 100 unit increment in the y variable. This means that the growth rate of this function is 100.

The table C also represents a linear function, for which each one unit increment in the x variable produces a 10 unit increment in the y variable. This means that the growth rate of this function is 10.

The table D on the other hand does not represent a linear function, since the growth rate is variable and increases for greater values of x. This means that as x grows larger, the growth rate of the function also grows larger, resulting in a much greater y value for very large x values if we compare it to a linear function, like the other options.

  C

Step-by-step explanation:

The function of table A can be written as ...

  y = 100x -92

__

The function of table B can be written as ...

  y = 10x +446

__

The function of table C can be written as ...

  y = (5/3)·3^x

__

The function of table D can be written as ...

  y = 2x +413

__

The exponential function of Table C will have the largest y-values for any value of x greater than 6.

Comment on the functions

When trying to determine the nature of the function, it is often useful to look at the differences of the y-values for consecutive x-values. Here, the first-differences are constant for all tables except C. That means functions A, B, D are linear functions.

If the first differences are not constant, one can look at second differences and at ratios. For table C, we notice that each y-value is 3 times the previous one. That constant ratio means the function is exponential, hence will grow faster than any linear function.

C.

Step-by-step explanation:

I just did the test.

D

Step-by-step explanation:

The answer is D because every time x increase by 1, the y is tripling. Making it so that as x gets larger and larger, the y will become the larger than the other choices.  

D

Step-by-step explanation:

The answer is D because every time x increase by 1, the y is tripling. Making it so that as x gets larger and larger, the y will become the larger than the other choices.  

c

Step-by-step explanation:

An exponential function is a function where the number is raised to a constant power

exponential function is usually in the form : f(x) =

a is positive and not equal to 1

x is a real number

to determine which option is an exponential function, determine which of the options have a common ratio

Option A :

28/7 = 4

49 / 28 = 1.75

option C

12 / 4 = 3

36 /12 = 3

the correct answer is C

Option C

Step-by-step explanation:

In this case, an exponential function is a function that has common ratio whereas it is called a linear function if it has common difference.

Option A:

Since the values of y in the given table have different ratio but common difference, therefore it is not a a linear and not an exponential function. Option A is is not correct.

Option B:

Since the values of y in the given table have different ratio but common difference, therefore it is not a a linear and not an exponential function. Option B is not correct.

In option C.

Since the given values of y in the table have a common ratio, it is said to be an exponential function.

Option C is correct.

In option D.

Since the values of y in the given table have different ratio but common difference, therefore it is not a a linear and not an exponential function. Option D is incorrect.