What is the molecular mass for a non-electrolyte if 35.0 g of it is dissolved in 45.0 grams of water and the solutions boiling point is 101.25oC? (The KB for H2O is .51°C/m)

The boiling point of water increases as the amount of impurities dissolved in it increases. For our purposes, we will consider the non-electrolyte to be the dissolved impurity. The change in the boiling point can be calculated using the equation:

where 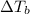is the change in boiling point, is the van ‘t Hoff factor (whose value denotes the number of particles each formula unit of the dissolved substance dissociates into in water), 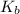is the boiling point elevation constant, and 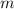is the molality (moles of solute/kilogram of solvent) of the solution.

Right off the bat, since we're dealing with a non-electrolyte, the dissolved substance can be assumed not to dissociate in water. So, our van ‘t Hoff factor, , would be 1 (by contrast, the for an ionic compound like NaCl would be 2 since, in water, NaCl would dissociate into two particles: one Na⁺ ion and one Cl⁻ ion). We're also given our 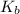, which is 0.51 °C/m.

Assuming the normal boiling point of pure water to be 100 °C (a defined value for sig fig purposes), the change in boiling point from having dissolved 35.0 g of the non-electrolyte can be obtained by subtracting 100 °C from the final—elevated—boiling point of 101.25 °C:

Now, recall what we're asked to determine: the molecular mass of the dissolved substance. There is one unknown left in the equation: the molality of the solution. Let's first solve for that:

Notice that we didn't include the i since its value is 1.

Now, what would happen if we multiplied our molality by the mass of water we've been given? We would be left with the moles of solute. And what are we asked to find? The molecular mass, or the mass per mole. We can accomplish this in two steps. Remember to convert your mass of water to kilograms:

And, finally, we divide the mass of our solute by the number of moles of solute:

Our answer to two significant figures (which is the number of sig figs to which our 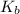is given) would be 320 g/mol.

Answer:

Step-by-step explanation:

The input force is 50 N. But it will not create not any change. No mechanical advantage is observed.

glycoproteins

Explanation:

A positive reaction for Molisch's test is given by almost all carbohydrates (exceptions include tetroses & trioses). It can be noted that even some glycoproteins and nucleic acids give positive results for this test (since they tend to undergo hydrolysis when exposed to strong mineral acids and form monosaccharides).

Answer:

Taking into accoun the ideal gas law, The volume of a container that contains 24.0 grams of N2 gas at 328K and 0.884 atm is 26.07 L.

An ideal gas is a theoretical gas that is considered to be composed of point particles that move randomly and do not interact with each other. Gases in general are ideal when they are at high temperatures and low pressures.

The pressure, P, the temperature, T, and the volume, V, of an ideal gas, are related by a simple formula called the ideal gas law:  

P×V = n×R×T

where P is the gas pressure, V is the volume that occupies, T is its temperature, R is the ideal gas constant, and n is the number of moles of the gas. The universal constant of ideal gases R has the same value for all gaseous substances.

Explanation:

In this case, you know:

P= 0.884 atm

V= ?

n= 0.857 moles (where 28 g/mole is the molar mass of N₂, that is, the amount of mass that the substance contains in one mole.)

R=0.082

T= 328 K

Replacing in the ideal gas law:

0.884 atm×V= 0.857 moles× 0.082 ×328 K

Solving:

V= 26.07 L

The volume of a container that contains 24.0 grams of N2 gas at 328K and 0.884 atm is 26.07 L.