1 cake and 6 pies
Step-by-step explanation:
Let c represent the number of cakes Alice and George can make. Likewise, let p represent the number of pies.
Then the amount of flour they need (in cups) is ...
3c + 2p . . . . cups of flour needed
And the amount of sugar needed is ...
2c + 1.5p . . . cups of sugar needed
__
They want to use all 15 cups of flour they have, and all 11 cups of sugar, so the amounts above need to match the amounts on hand:
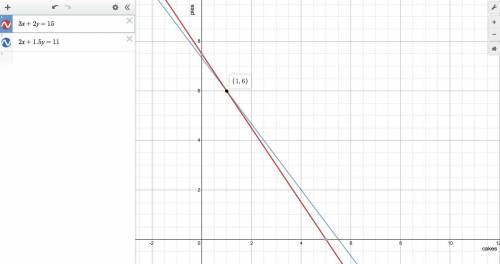
3c + 2p = 15
2c + 1.5p = 11
We can solve these equations various ways. One of my favorite is to use a graphing calculator. (See attached) It tells us that Alice and George can make 1 cake and 6 pies with the flour and sugar they have.
_____
If you want to solve these equations algebraically, there are several methods for that, too. Here, we can multiply the first one by 2/3 and subtract the result from the second one:
(2c +1.5p) -(2/3)(3c +2p) = (11) -(2/3)(15)
2c +3/2p -2c -4/3p = 11 -10 . . . . . eliminate parentheses
1/6p = 1 . . . . . . . . . . . . . . . . . . . . . .collect terms
p = 6 . . . . . . . . . . . . . . . . . . . . . . . . multiply by 6
Substituting into the first equation gives ...
3c +2·6 = 15 . . . substitute 6 for p
3c = 3 . . . . . . . . subtract 12
c = 1 . . . . . . . . . . divide by 3
These values tell us Alice and George can make 1 cake and 6 pies with the flour and sugar they have.