The rocket hits the gorund after approximately 10.71 seconds.
Step-by-step explanation:
The height of the rocket y in feet x seconds after launch is given by the equation:
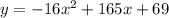
And we want to find the time in which the rocket will hit the ground.
When it hits the ground, its height above ground will be 0. Hence, we can let y = 0 and solve for x:
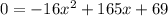
We can use the quadratic formula:
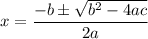
In this case, a = -16, b = 165, and c = 69.
Substitute:
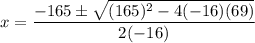
Evaluate:
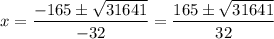
Hence, our solutions are:
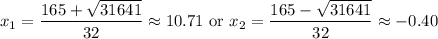
Since time cannot be negative, we can ignore the first answer.
So, the rocket hits the gorund after approximately 10.71 seconds.