14/35 as a equivalent fraction, №17886063, 16.09.2022 07:28

Mathematics

14/35 as a equivalent fraction

Step-by-step answer

P Answered by PhD

2

2/5 because I divided by 7/7 to get an equivalent fraction

Step-by-step explanation:

Mathematics

Which of the following fraction pairs is equivalent? 15/25 and 24/30 12/35 and 14/35 14/21 and 8/20 18/45 and 14/35

Step-by-step answer

P Answered by Specialist

2

18/45 and 14/35

Step-by-step explanation:

15/25 are not equivalent fractions

12/35 are also not equivalent

14/21 are not equivalent either

18/45 and 14/35 are the only equivalent fractions.

Mathematics

Which of the following fraction pairs is equivalent? 15/25 and 24/30 12/35 and 14/35 14/21 and 8/20 18/45 and 14/35

Step-by-step answer

P Answered by Master

2

18/45 and 14/35

Step-by-step explanation:

15/25 are not equivalent fractions

12/35 are also not equivalent

14/21 are not equivalent either

18/45 and 14/35 are the only equivalent fractions.

Business

Quarter ($000) Net Income Operating Activities, Cash Flows Provided By or Used In Depreciation Adjustments to net income Changes in accounts receivable Changes in liabilities Changes in inventories Changes in other operating activities Total Cash Flow from Operating Activities Investing Activities, Cash Flows Provided By or Used In Capital expenditures Investments Other cash flows from investing activities Total Cash Flows from Investing Activities Financing Activities, Cash Flows Provided By or Used In Dividends paid Sale or purchase of stock

Step-by-step answer

P Answered by Specialist

Find full question attached

Answer and Explanation:

Answer and explanation attached

Please refer to figures from the question for our answers

Quarter ($000) Net Income Operating Activities, Cash Flows Provided By or Used In Depreciation Adjus

Business

Quarter ($000) Net Income Operating Activities, Cash Flows Provided By or Used In Depreciation Adjustments to net income Changes in accounts receivable Changes in liabilities Changes in inventories Changes in other operating activities Total Cash Flow from Operating Activities Investing Activities, Cash Flows Provided By or Used In Capital expenditures Investments Other cash flows from investing activities Total Cash Flows from Investing Activities Financing Activities, Cash Flows Provided By or Used In Dividends paid Sale or purchase of stock

Step-by-step answer

P Answered by Specialist

Find full question attached

Answer and Explanation:

Answer and explanation attached

Please refer to figures from the question for our answers

Mathematics

1. find the digit that makes 3,71_ divisible by 9. a. 3 b. 7 c. 1 d. 5 2.list all the factors of the number 30. a. 1, 2, 3, 5, 6, 10, 15, 30 b. 2, 3, 4, 10, 20, 30, 40 c. 1, 2, 4, 5, 10, 15, 30 d. 1, 2, 4, 5, 8, 10, 20, 40 3. find the prime factorization of the number 168. a. 24 x 3 x 7 b. 23 x 3 x 7 c. 24 x 33 x 13 d. 23 x 33 x 7 4. find the gcf of the numbers 140 and 180. a. 20 b. 90 c. 30 d. 10 5. the weights of 3 bags containing footballs are 15 oz, 30 oz, and 60 oz. the greatest common factor of 15, 30, and 60 gives the weight of each ball

Step-by-step answer

P Answered by PhD

64

QUESTION 1

We want to find the digit that should fill the blank space to make

3,71-

divisible by 9.

If a number is divisible by 9 then the sum of the digits should be a multiple of 9.

The sum of the given digits is,

3 + 7 + 1 = 11

Since

11 + 7 = 18

which is a multiple of 9.

This means that

3,717

is divisible by 9.

The correct answer is B

QUESTION 2

The factors of the number 30 are all the numbers that divides 30 exactly without a remainder.

These numbers are ;

1,2,3,5,6,10,15,30

The correct answer is A.

QUESTION 3.

We want to find the prime factorization of the number 168.

The prime numbers that are factors of 168 are

$2,3 \: and \: 7$

We can write 168 as the product of these three prime numbers to obtain,

$168={2}^{3}\times 3\times7$

We can also use the factor tree as shown in the attachment to write the prime factorization of 168 as

$168 ={2}^{3}\times 3\times7$

The correct answer is B.

QUESTION 4.

We want to find the greatest common factor of

$140\:\:and\:\:180$

We need to express each of these numbers as a product of prime factors.

The prime factorization of 140 is

$140={2}^{2}\times 5\times7.$

The prime factorization of 180 is

$180={2}^{2} \times{3}^{2}\times5.$

The greatest common factor is the product of the least degree of each common factor.

$GCF={2}^{2}\times5$

GCF=20

The correct answer is A.

QUESTION 5.

We want to find the greatest common factor of

$15,30\: and\:60.$

We need to first find the prime factorization of each number.

The prime factorization of 15 is

$15=3\times5.$

The prime factorization of 30 is

$30=2\times 3\times 5.$

The prime factorization of 60 is

$60={2}^{2}\times3 \times5$

The greatest common factor of these three numbers is the product of the factors with the least degree that is common to them.

$GCF=3 \times5$

GCF=15

The correct answer is C.

QUESTION 6

We want to determine which of the given fractions is equivalent to

$\frac{3}{8}.$

We must therefore simplify each option,

$A.\: \: \frac{15}{32}=\frac{15}{32}$

$B.\:\:\frac{12}{32}=\frac{4\times 3}{4\times8}=\frac{3}{8}$

$C.\:\:\:\:\frac{12}{24}=\frac{12\times1}{12\times 2}=\frac{1}{2}$

$D.\:\:\frac{9}{32}=\frac{9}{32}$

The simplification shows that

$\frac{12}{32}\equiv \frac{3}{8}$

The correct answer is B.

QUESTION 7.

We want to express

$\frac{10}{22}$

in the simplest form.

We just have to cancel out common factors as follows.

$\frac{10}{22}=\frac{2\times5}{2 \times11}$

This simplifies to,

$\frac{10}{22}=\frac{5}{11}$

The correct answer is C.

QUESTION 8.

We were given that Justin visited of the states.

The question requires that we express as a fraction of 50.

This will give us

$\frac{25}{50}=\frac{25\times1}{25\times2}$

We must cancel out the common factors to have our fraction in the simplest form.

$\frac{25}{50}=\frac{1}{2}$

The correct answer is C.

QUESTION 9.

We want to write

$2\frac{5}{8}$

as an improper fraction.

We need to multiply the 2 by the denominator which is 8 and add the product to 5 and then express the result over 8.

This gives us,

$2 \frac{5}{8}=\frac{2\times8+5}{8}$

this implies that,

$2\frac{5}{8}=\frac{16+5}{8}$

$2\frac{5}{8}=\frac{21}{8}$

Sarah needed

$\frac{21}{8}\:\:yards$

The correct answer is D.

QUESTION 10

See attachment

QUESTION 11

We wan to write

$3\: and\:\:\frac{7}{8}$

as an improper fraction.

This implies that,

$3+\frac{7}{8}=3\frac{7}{8}$

To write this as a mixed number, we have,

$3\frac{7}{8}=\frac{3\times8+7}{8}$

This implies that,

$3\frac{7}{8}=\frac{24+7}{8}$

This gives

$3\frac{7}{8}=\frac{31}{8}$

The correct answer is B.

QUESTION 12

We want to find the LCM of and using prime factorization.

The prime factorization of 30 is $30=2\times 3\times 5$

The prime factorization of 46 is $40=2\times 23$ .

The LCM is the product of the common factors with the highest degrees. This gives us,

$LCM=2\times \times3 5\times 23$

LCM=690

The correct answer is D.

QUESTION 13

We want to find the least common multiple of 3,6 and 7.

The prime factorization of is .

The prime factorization of 6 is $6=2\times 3$ .

The prime factorization of 7 is .

The LCM is the product of the common factors with the highest degrees. This gives us,

$LCM=2\times3 \times7$

LCM=42 .

The LCM is 42, therefore 42 days will pass before all three bikes will at the park on the same day again.

The correct answer is B.

See attachment for continuation.

1. find the digit that makes 3,71_ divisible by 9. a. 3 b. 7 c. 1 d. 5 2.list all the factors of the

Mathematics

1. find the digit that makes 3,71_ divisible by 9. a. 3 b. 7 c. 1 d. 5 2.list all the factors of the number 30. a. 1, 2, 3, 5, 6, 10, 15, 30 b. 2, 3, 4, 10, 20, 30, 40 c. 1, 2, 4, 5, 10, 15, 30 d. 1, 2, 4, 5, 8, 10, 20, 40 3. find the prime factorization of the number 168. a. 24 x 3 x 7 b. 23 x 3 x 7 c. 24 x 33 x 13 d. 23 x 33 x 7 4. find the gcf of the numbers 140 and 180. a. 20 b. 90 c. 30 d. 10 5. the weights of 3 bags containing footballs are 15 oz, 30 oz, and 60 oz. the greatest common factor of 15, 30, and 60 gives the weight of each ball

Step-by-step answer

P Answered by PhD

64

QUESTION 1

We want to find the digit that should fill the blank space to make

3,71-

divisible by 9.

If a number is divisible by 9 then the sum of the digits should be a multiple of 9.

The sum of the given digits is,

3 + 7 + 1 = 11

Since

11 + 7 = 18

which is a multiple of 9.

This means that

3,717

is divisible by 9.

The correct answer is B

QUESTION 2

The factors of the number 30 are all the numbers that divides 30 exactly without a remainder.

These numbers are ;

1,2,3,5,6,10,15,30

The correct answer is A.

QUESTION 3.

We want to find the prime factorization of the number 168.

The prime numbers that are factors of 168 are

$2,3 \: and \: 7$

We can write 168 as the product of these three prime numbers to obtain,

$168={2}^{3}\times 3\times7$

We can also use the factor tree as shown in the attachment to write the prime factorization of 168 as

$168 ={2}^{3}\times 3\times7$

The correct answer is B.

QUESTION 4.

We want to find the greatest common factor of

$140\:\:and\:\:180$

We need to express each of these numbers as a product of prime factors.

The prime factorization of 140 is

$140={2}^{2}\times 5\times7.$

The prime factorization of 180 is

$180={2}^{2} \times{3}^{2}\times5.$

The greatest common factor is the product of the least degree of each common factor.

$GCF={2}^{2}\times5$

GCF=20

The correct answer is A.

QUESTION 5.

We want to find the greatest common factor of

$15,30\: and\:60.$

We need to first find the prime factorization of each number.

The prime factorization of 15 is

$15=3\times5.$

The prime factorization of 30 is

$30=2\times 3\times 5.$

The prime factorization of 60 is

$60={2}^{2}\times3 \times5$

The greatest common factor of these three numbers is the product of the factors with the least degree that is common to them.

$GCF=3 \times5$

GCF=15

The correct answer is C.

QUESTION 6

We want to determine which of the given fractions is equivalent to

$\frac{3}{8}.$

We must therefore simplify each option,

$A.\: \: \frac{15}{32}=\frac{15}{32}$

$B.\:\:\frac{12}{32}=\frac{4\times 3}{4\times8}=\frac{3}{8}$

$C.\:\:\:\:\frac{12}{24}=\frac{12\times1}{12\times 2}=\frac{1}{2}$

$D.\:\:\frac{9}{32}=\frac{9}{32}$

The simplification shows that

$\frac{12}{32}\equiv \frac{3}{8}$

The correct answer is B.

QUESTION 7.

We want to express

$\frac{10}{22}$

in the simplest form.

We just have to cancel out common factors as follows.

$\frac{10}{22}=\frac{2\times5}{2 \times11}$

This simplifies to,

$\frac{10}{22}=\frac{5}{11}$

The correct answer is C.

QUESTION 8.

We were given that Justin visited of the states.

The question requires that we express as a fraction of 50.

This will give us

$\frac{25}{50}=\frac{25\times1}{25\times2}$

We must cancel out the common factors to have our fraction in the simplest form.

$\frac{25}{50}=\frac{1}{2}$

The correct answer is C.

QUESTION 9.

We want to write

$2\frac{5}{8}$

as an improper fraction.

We need to multiply the 2 by the denominator which is 8 and add the product to 5 and then express the result over 8.

This gives us,

$2 \frac{5}{8}=\frac{2\times8+5}{8}$

this implies that,

$2\frac{5}{8}=\frac{16+5}{8}$

$2\frac{5}{8}=\frac{21}{8}$

Sarah needed

$\frac{21}{8}\:\:yards$

The correct answer is D.

QUESTION 10

See attachment

QUESTION 11

We wan to write

$3\: and\:\:\frac{7}{8}$

as an improper fraction.

This implies that,

$3+\frac{7}{8}=3\frac{7}{8}$

To write this as a mixed number, we have,

$3\frac{7}{8}=\frac{3\times8+7}{8}$

This implies that,

$3\frac{7}{8}=\frac{24+7}{8}$

This gives

$3\frac{7}{8}=\frac{31}{8}$

The correct answer is B.

QUESTION 12

We want to find the LCM of and using prime factorization.

The prime factorization of 30 is $30=2\times 3\times 5$

The prime factorization of 46 is $40=2\times 23$ .

The LCM is the product of the common factors with the highest degrees. This gives us,

$LCM=2\times \times3 5\times 23$

LCM=690

The correct answer is D.

QUESTION 13

We want to find the least common multiple of 3,6 and 7.

The prime factorization of is .

The prime factorization of 6 is $6=2\times 3$ .

The prime factorization of 7 is .

The LCM is the product of the common factors with the highest degrees. This gives us,

$LCM=2\times3 \times7$

LCM=42 .

The LCM is 42, therefore 42 days will pass before all three bikes will at the park on the same day again.

The correct answer is B.

See attachment for continuation.

Mathematics

Write each of the following percents in words. a. 5% b. 34% c. 143% d. 500% for each comparison, write the corresponding percent. a. 7 out of 100 b. 76 out of 100 c. 430 compared to 100 d. 600 compared to 100 for each fraction, write the equivalent percent. a. 6⁄100 b. 57⁄100 c. 357⁄100 d. 100⁄100 compare each percent to 1 by inserting the symbol , , or = to make a true statement. a. 9.7% 1 b. 80% 1 c. 127% 1 d. 100% 1 change each percent to a decimal or a mixed decimal. a. 43% b. 21⁄2% c. 13.6% d. 521% change each decimal or mixed decimal to a

Step-by-step answer

P Answered by Master

62

Please, see the attached files.

Step-by-step explanation:

Please, see the attached files.

Mathematics

Write each of the following percents in words. a. 5% b. 34% c. 143% d. 500% for each comparison, write the corresponding percent. a. 7 out of 100 b. 76 out of 100 c. 430 compared to 100 d. 600 compared to 100 for each fraction, write the equivalent percent. a. 6⁄100 b. 57⁄100 c. 357⁄100 d. 100⁄100 compare each percent to 1 by inserting the symbol , , or = to make a true statement. a. 9.7% 1 b. 80% 1 c. 127% 1 d. 100% 1 change each percent to a decimal or a mixed decimal. a. 43% b. 21⁄2% c. 13.6% d. 521% change each decimal or mixed decimal to a

Step-by-step answer

P Answered by Master

62

Please, see the attached files.

Step-by-step explanation:

Please, see the attached files.

Mathematics

Change the decimal to a fraction. reduce the fraction if possible. a. 0.578 b. 3.5 c. 2.73 d. 0.4211 change the fraction to a decimal. a. 6⁄100 b. 43⁄100 c. 3⁄10 d. 4 23⁄1,000 calculate the equivalent decimals for the following fractions. a. 1⁄4 b. 2⁄5 c. 2⁄3 d. 3⁄4 perform the indicated operation. a. 18.67 + 3.456 + 0.2 + 3.21 b. 3.256 + 4.21 + 3.009 + 0.35 c. 7 – 3.06 d. 62.98 – 3.555 e. 5.3 × 12 f. 4.35 × 2.11 g. 56⁄0.7 h. 5.6⁄7 the distance around a circle is called the circumference. the distance across a circle is called the diameter. to

Step-by-step answer

P Answered by PhD

16

QUESTION 1a

We want to change 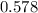0.578 to a fraction in the simplest form.

We need repeatedly multiply by multiples of 10, until we obtain an integer(the least integer). We then divide by the same value that we used to multiply to get,

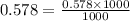
$0.578=\frac{0.578\times 1000}{1000}$

This implies that,

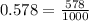
$0.578=\frac{578}{1000}$

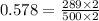
$0.578=\frac{289\times 2}{500\times 2}$

We cancel out the common factors to get,

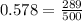
$0.578=\frac{289}{500}$

QUESTION 1b

We want to convert 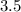3.5 to a fraction in the simplest form.

We need repeatedly multiply by multiples of 10, until we obtain an integer(the least integer). We then divide by the same value that we used to multiply to get,

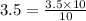
$3.5=\frac{3.5\times 10}{10}$

This implies that,

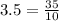
$3.5=\frac{35}{10}$

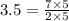
$3.5=\frac{7\times 5}{2\times 5}$

We cancel out the common factors to get,

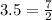
$3.5=\frac{7}{2}$

Or as mixed numbers, we have

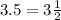
$3.5=3\frac{1}{2}$

QUESTION 1c

We want to convert 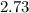2.73 to a fraction in the simplest form.

We need repeatedly multiply by multiples of 10, until we obtain an integer(the least integer). We then divide by the same value that we used to multiply to get,

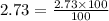
$2.73=\frac{2.73\times 100}{100}$

This implies that,

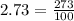
$2.73=\frac{273}{100}$

Or as mixed numbers, we have

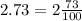
$2.73=2\frac{73}{100}$

QUESTION 1d

We want to change 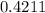0.4211 to a fraction in the simplest form.

We need repeatedly multiply by multiples of 10, until we obtain an integer(the least integer). We then divide by the same value that we used to multiply to get,

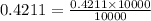
$0.4211=\frac{0.4211\times 10000}{10000}$

This implies that,

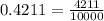
$0.4211=\frac{4211}{10000}$

Question 2a

We want to convert 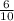$\frac{6}{10}$ into decimal.

This fraction is having a denominator of 10 so we just have to move the decimal point back once to get,

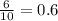
$\frac{6}{10}=0.6$

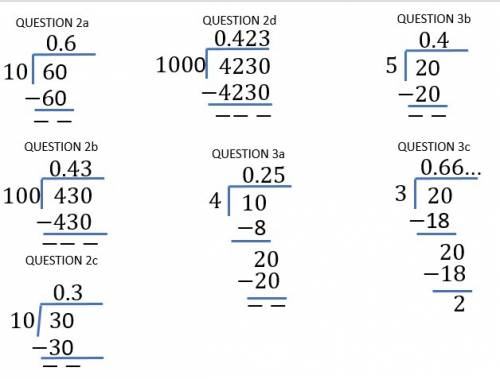
Check attachment for long division.

QUESTION 2b

We want to convert 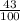$\frac{43}{100}$ into decimal.

This fraction is having a denominator of 100 so we just have to move the decimal point back twice to get,

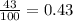
$\frac{43}{100}=0.43$

Check attachment for long division.

QUESTION 2c

We want to change 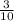$\frac{3}{10}$ into decimal.

This fraction is having a denominator of 10 so we just have to move the decimal point back once to get,

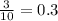
$\frac{3}{10}=0.3$

Check attachment for long division.

QUESTION 2d

The given fraction is 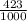$\frac{423}{1000}$ .

This fraction is having a denominator of 1000 so we just have to move the decimal point back three times to obtain,

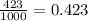
$\frac{423}{1000}=0.423$

Check attachment for long division.

QUESTION 3a

The given fraction is 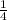$\frac{1}{4}$ .

We can make the denominator 100 by multiplying both the numerator and the denominator by 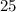to obtain,

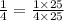
$\frac{1}{4} =\frac{1\times 25}{4\times 25}$

This implies that,

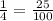
$\frac{1}{4} =\frac{25}{100}$

We move the decimal point back twice to obtain,

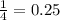
$\frac{1}{4} =0.25$

See attachment for long division

QUESTION 3b

The given fraction is 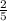$\frac{2}{5}$ .

We can make the denominator 10 by multiplying both the numerator and the denominator by 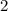to obtain,

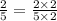
$\frac{2}{5} =\frac{2\times 2}{5\times 2}$

This implies that,

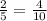
$\frac{2}{5} =\frac{4}{10}$

We move the decimal point back twice to obtain,

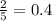
$\frac{2}{5} =0.4$

See attachment for long division

QUESTION 3c

We want to change 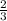$\frac{2}{3}$ into decimals.

We use long division as shown in the attachment to obtain;

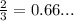
$\frac{2}{3}=0.66...$

QUESTION 3d

The given fraction is 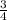$\frac{3}{4}$ .

We can make the denominator 100 by multiplying both the numerator and the denominator by 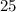to obtain,

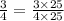
$\frac{3}{4} =\frac{3\times 25}{4\times 25}$

This implies that,

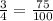
$\frac{3}{4} =\frac{75}{100}$

We move the decimal point back twice to obtain,

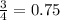
$\frac{3}{4} =0.75$

QUESTION 4a

We want to simplify

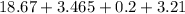
18.67+3.465+0.2+3.21

We arrange to obtain,

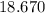
18.670

3.465

0.200

+ 3.210

----------------------------

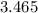
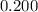
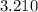
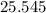
25.545

----------------------------

QUESTION 4b

We want to simplify

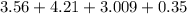
3.56+4.21+3.009+0.35

We rearrange and carry out the operation as follows;

3.256

4.210

3.009

+ 0.350

----------------------

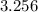
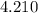
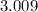
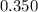
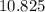
10.825

-----------------------

QUESTION 4c

We want to simplify

7-3.06

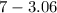
We rearrange and perform the operation as follows;

7.00

- 3.06

--------------------

3.94

--------------------

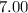
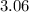
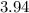
QUESTION 4d

We want to simplify,

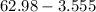
62.98-3.555

We rearrange and carry out the operations as follows;

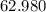
62.980

-3.555

---------------------

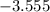
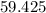
59.425

---------------------

QUESTION 4e

We want to simplify the product;

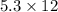
$5.3\times 12$

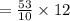
$=\frac{53}{10}\times 12$

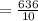
$=\frac{636}{10}$

=63.6

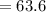
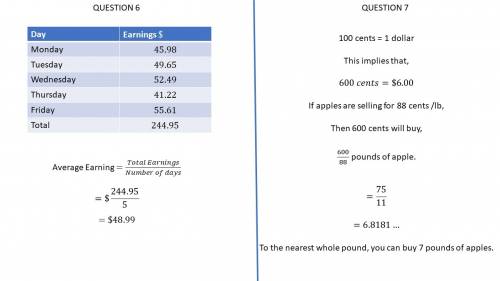
The rest of the solutions will be in the attachment

$Change the decimal to a fraction. reduce the fraction if possible. a. 0.578 b. 3.5 c. 2.73 d. 0.4211$
$Change the decimal to a fraction. reduce the fraction if possible. a. 0.578 b. 3.5 c. 2.73 d. 0.4211$
$Change the decimal to a fraction. reduce the fraction if possible. a. 0.578 b. 3.5 c. 2.73 d. 0.4211$
$Change the decimal to a fraction. reduce the fraction if possible. a. 0.578 b. 3.5 c. 2.73 d. 0.4211$

14/35 as a equivalent fraction

Step-by-step answer

Faq

Try asking the Studen AI a question.