Part I
Let
x--------> represent the length of the cuts
For any given cut, the available distance is reduced by twice the length of the cut.
So
we can create the following equations for length, width, and height.
width: w = 12 - 2x
length: l = 18 - 2x
height: h = x
Part II
v = l * w * h
v = (18 - 2x)(12 - 2x)x
v = (216 - 36x - 24x + 4x^2)x
v = (216 - 60x + 4x^2)x
v = 216x - 60x^2 + 4x^3
v = 4x^3 - 60x^2 + 216x
Part III
The length of the cut has to be greater than 0 and less than half the length of the smallest dimension of the cardboard
So
0 < x < 6
If we use a value of x=1 in
we get a volume of:
v = 4x^3 - 60x^2 + 216x
v = 4*1^3 - 60*1^2 + 216*1
v = 4*1 - 60*1 + 216
v = 4 - 60 + 216v = 160 in³
Too small,
so
let's try x=2 in
v = 4x^3 - 60x^2 + 216x
v = 4*2^3 - 60*2^2 + 216*2
v = 4*8 - 60*4 + 216*2
v = 32 - 240 + 432v = 224 in³
And that's the desired volume.
So
let's choose a value of x=2 in
Reason?
It meets the inequality of
0 < x < 6
and it also gives the desired volume of 224 cubic inches.
Part IV
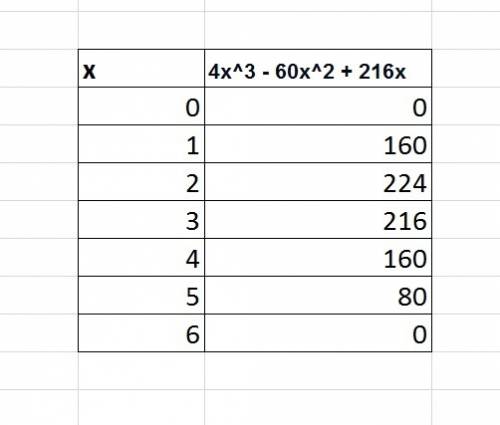
the table in the attached figure
Part V
Based on your table, what x-value creates a box with a volume of 224 in3?
based on the table
the answer Part V is
x=2 in
Part VI
width: w = 12 - 2x-----> w=12-2*2----> w=8 in
length: l = 18 - 2x-----> l=18-2*2-----> l=14 in
height: h = x----------> h=x------> h=2 in