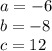Mathematics : asked on igivebirth4170

04.06.2020

Factor quadratic equation. 6x squared +10-56

Step-by-step answer

24.06.2023, solved by verified expert

Bhaskar Singh Bora

p PhD

Mathematics, Physics. Q&A Expert

14 251

23 753 answers

4.8 rating

Unlock the full answer

Step-by-step explanation:

Factor using the Quadratic formula

It is was helpful?

Helpful Useless

Faq

Mathematics

Factor quadratic equation. 6x squared +10-56

Step-by-step answer

P Answered by PhD

$x=\frac{±\sqrt{69} }{3}$

Step-by-step explanation:

Factor using the Quadratic formula

Mathematics

Question 1 solve for x using the quadratic formula: x2 − 6x + 9 = 0 x equals negative b plus or minus the square root of b squared minus 4 times a times c, all over 2 times a x = 6 x = 3 x = 1 x = 0 question 2 solve: 49x2 − 60 = 0 round your answer to the nearest hundredth. x = 0 x = −3.32 and x = 3.32 x = −1.11 and x = 1.11 x = −0.82 and x = 0.82 question 3 when the solution of x2 − 9x − 6 is expressed as 9 plus or minus the square root of r, all over 2, what is the value of r? x equals negative b plus or minus the square root of b squared minus

Step-by-step answer

P Answered by Master

Part 1) x=3

Part 2) x = −1.11 and x = 1.11

Part 3) 105

Part 4) a = −6, b = 9, c = −7

Part 5) x equals 5 plus or minus the square root of 33, all over 2

Part 6) In the procedure

Part 7) 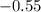-0.55

Part 8) The denominator is 2

Part 9) a = −6, b = −8, c = 12

Step-by-step explanation:

we know that

The formula to solve a quadratic equation of the form 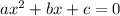$ax^{2} +bx+c=0$ is equal to

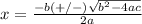
$x=\frac{-b(+/-)\sqrt{b^{2}-4ac}} {2a}$

Part 1)

in this problem we have

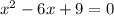
$x^{2} -6x+9=0$

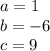
$a=1\\b=-6\\c=9$

substitute in the formula

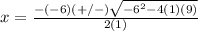
$x=\frac{-(-6)(+/-)\sqrt{-6^{2}-4(1)(9)}} {2(1)}$

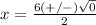
$x=\frac{6(+/-)\sqrt{0}} {2}$

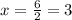
$x=\frac{6} {2}=3$

Part 2) in this problem we have

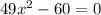
$49x^{2} -60=0$

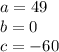
$a=49\\b=0\\c=-60$

substitute in the formula

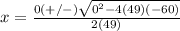
$x=\frac{0(+/-)\sqrt{0^{2}-4(49)(-60)}} {2(49)}$

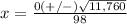
$x=\frac{0(+/-)\sqrt{11,760}} {98}$

x=(+/-)1.11

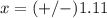
Part 3) When the solution of x2 − 9x − 6 is expressed as 9 plus or minus the square root of r, all over 2, what is the value of r?

in this problem we have

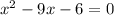
$x^{2} -9x-6=0$

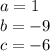
$a=1\\b=-9\\c=-6$

substitute in the formula

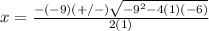
$x=\frac{-(-9)(+/-)\sqrt{-9^{2}-4(1)(-6)}} {2(1)}$

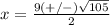
$x=\frac{9(+/-)\sqrt{105}} {2}$

therefore

r=105

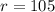
Part 4) What are the values a, b, and c in the following quadratic equation?

−6x2 = −9x + 7

in this problem we have

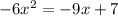
$-6x^{2}=-9x+7$

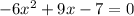
$-6x^{2}+9x-7=0$

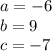
$a=-6\\b=9\\c=-7$

Part 5) Use the quadratic formula to find the exact solutions of x2 − 5x − 2 = 0.

In this problem we have

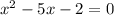
$x^{2} -5x-2=0$

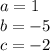
$a=1\\b=-5\\c=-2$

substitute in the formula

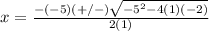
$x=\frac{-(-5)(+/-)\sqrt{-5^{2}-4(1)(-2)}} {2(1)}$

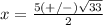
$x=\frac{5(+/-)\sqrt{33}} {2}$

therefore

x equals 5 plus or minus the square root of 33, all over 2

Part 6) Quadratic Formula proof

we have

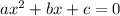
$ax^{2} +bx+c=0$

Divide both sides by a

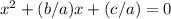
$x^{2} +(b/a)x+(c/a)=0$

Complete the square

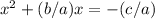
$x^{2} +(b/a)x=-(c/a)$

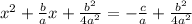
$x^{2} +\frac{b}{a}x+\frac{b^{2}}{4a^{2}} =-\frac{c}{a}+\frac{b^{2}}{4a^{2}}$

Rewrite the perfect square trinomial on the left side of the equation as a binomial squared

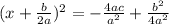
$(x+\frac{b}{2a})^{2}=-\frac{4ac}{a^{2}}+\frac{b^{2}}{4a^{2}}$

Find a common denominator on the right side of the equation

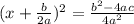
$(x+\frac{b}{2a})^{2}=\frac{b^{2}-4ac}{4a^{2}}$

Take the square root of both sides of the equation

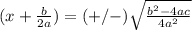
$(x+\frac{b}{2a})=(+/-)\sqrt{\frac{b^{2}-4ac}{4a^{2}}}$

Simplify the right side of the equation

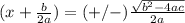
$(x+\frac{b}{2a})=(+/-)\frac{\sqrt{b^{2}-4ac}}{2a}$

Subtract the quantity b over 2 times a from both sides of the equation

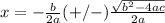
$x=-\frac{b}{2a}(+/-)\frac{\sqrt{b^{2}-4ac}}{2a}$

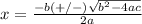
$x=\frac{-b(+/-)\sqrt{b^{2}-4ac}} {2a}$

Part 7) in this problem we have

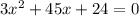
$3x^{2} +45x+24=0$

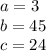
$a=3\\b=45\\c=24$

substitute in the formula

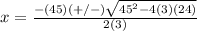
$x=\frac{-(45)(+/-)\sqrt{45^{2}-4(3)(24)}} {2(3)}$

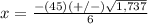
$x=\frac{-(45)(+/-)\sqrt{1,737}} {6}$

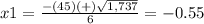
$x1=\frac{-(45)(+)\sqrt{1,737}} {6}=-0.55$

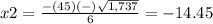
$x2=\frac{-(45)(-)\sqrt{1,737}} {6}=-14.45$

therefore

The other solution is

-0.55

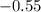
Part 8) in this problem we have

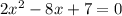
$2x^{2} -8x+7=0$

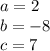
$a=2\\b=-8\\c=7$

substitute in the formula

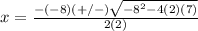
$x=\frac{-(-8)(+/-)\sqrt{-8^{2}-4(2)(7)}} {2(2)}$

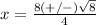
$x=\frac{8(+/-)\sqrt{8}} {4}$

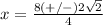
$x=\frac{8(+/-)2\sqrt{2}} {4}$

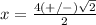
$x=\frac{4(+/-)\sqrt{2}} {2}$

therefore

The denominator is 2

Part 9) What are the values a, b, and c in the following quadratic equation?

−6x2 − 8x + 12

in this problem we have

$-6x^{2} -8x+12=0$

$a=-6\\b=-8\\c=12$

Mathematics

Solve the equation using the quadratic formula.x squared minus 4 x plus 3 equals 0 (1 point)x equals 2 semicolon x equals 4x equals 0 semicolon x equals 4x equals 1 semicolon x equals 3x equals negative 1 semicolon x equals 92. solve the equation using the quadratic formula. x squared plus 10 x equals negative 25 (1 point)x equals 5x equals negative 5x equals 15x equals 253. using the discriminant, determine the number of real solutions.negative 4 x squared plus 20 x minus 25 equals 0 (1 point)no real solutionsone real solutiontwo real solutions4.

Step-by-step answer

P Answered by Master

1: x=3, x=1
2: x= -5
3: There are 2 real solutions.
4: There are 2 real solutions.
5: There are no real solutions.
6. There is 1 real solution.
7. $x=\frac{2\pm \sqrt{10}}{3}$
8. x= -6, x = -2
9. x = -1/6, x=1
10. $x=\frac{3\pm \sqrt{5}}{2}$

Explanation:
1. The quadratic formula is
$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$
Substituting our known information we have:
$x=\frac{--4\pm \sqrt{(-4)^2-4(1)(3)}}{2(1)}
\\
\\=\frac{4\pm \sqrt{16-12}}{2}=\frac{4\pm \sqrt{4}}{2}=\frac{4\pm2}{2}
\\
\\=\frac{4+2}{2},\frac{4-2}{2}=\frac{6}{2},\frac{2}{2}=3,1$
2. Rewriting the quadratic in standard form we have x²+10x-25=0. Substituting this into the quadratic formula gives us:
$x=\frac{-10\pm \sqrt{10^2-4(1)(25)}}{2(1)}=\frac{-10\pm \sqrt{100-100}}{2}
\\
\\=\frac{-10\pm \sqrt{0}}{2}=\frac{-10\pm0}{2}=\frac{-10}{2}=-5$
3. The discriminant is b²-4ac. For this problem, that is 20²-4(-4)(25)=400--400=800. Since this is greater than 0, there are 2 real solutions.
4. The discriminant in this problem is 7²-4(2)(-15)=49--120=49+120=169. This is greater than 0, so there are 2 real solutions.
5. The discriminant in this problem is 1²-4(-2)(-28)=1-224=-223. Since this is less than 0, there are no real solutions.
6. If the discriminant of a quadratic is 0, then by definition there is 1 real solution.
7. Rewriting the quadratic we have 3x²-4x-2=0. Using the quadratic formula we have:
$x=\frac{--4\pm \sqrt{(-4)^2-4(3)(-2)}}{2(3)}=\frac{4\pm \sqrt{16--24}}{6}
\\
\\=\frac{4\pm \sqrt{40}}{6}=\frac{4\pm 2\sqrt{10}}{6}=\frac{2\pm \sqrt{10}}{3}$
8. Factoring this trinomial we want factors of 12 that sum to 8. 6*2 = 12 and 6+2=8, so those are our factors. This gives us:
(x+6)(x+2)=0
Using the zero product property we know that either x+6=0 or x+2=0. Solving these equations we get x= -6 or x= -2.
9. Factoring this trinomial we want factors of 6(-1)=-6 that sum to -5. (-6)(1)=-6 and -6+1=-5, so this is how we "split up" the x term:
6x²-6x+1x-1=0
We group together the first two and the last two terms:
(6x²-6x)+(1x-1)=0
Factor the GCF out of each group. In the first group, that is 6x:
6x(x-1)+(1x-1)=0
In the second group, the GCF is 1:
6x(x-1)+1(x-1)=0
Both terms have a factor of (x-1), so we can factor it out:
(x-1)(6x+1)=0
Using the zero product property, we know either x-1=0 or 6x+1=0. Solving these equations we get x=1 or x=-1/6.
10. Substituting our information into the quadratic formula we get:
$x=\frac{--3\pm \sqrt{(-3)^2-4(1)(1)}}{2(1)}=\frac{3\pm \sqrt{9-4}}{2}
\\
\\=\frac{3\pm \sqrt{5}}{2}$

Mathematics

Step-by-step answer

P Answered by Master

Mathematics

Answer these three questions for 100 points Question 1) Identifying the values a, b, and c is the first step in using the Quadratic Formula to find solution(s) to a quadratic equation. What are the values a, b, and c in the following quadratic equation? −6x2 = −9x + 7 A) a = 9, b = 7, c = 6 B) a = −9, b = 7, c = −6 C) a = −6, b = 9, c = −7 D) a = −6, b = −9, c = 7 Question 2) Identifying the values a, b, and c is the first step in using the Quadratic Formula to find solution(s) to a quadratic equation. What are the values a, b, and c in the following

Step-by-step answer

P Answered by PhD

C, A, D

edit - sorry the title was wrong earlier

Step-by-step explanation:

Question 1

in the quadratic formula, the equation is in the format of ax^2 + bx + c

so rearrange this equation so all values are on one side

-6x^2 = -9x + 7

-6x^2 + 9x - 7 =0

so a = -6, b = 9, c = -7

answer = C

Question 2

note that all the values are already on one side for this, so repeat the process from question 1 where the equation is in the format of ax^2 + bx + c

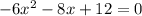
the equation = −6x2 − 8x + 12 = 0

so a = -6, b = -8, c = 12

answer = A

Question 3

(see picture below for steps)

following the same process above, a = 4, b = 45, and c = 24, so plug these values in the quadratic equation shown in the picture below

so you get the answers x = -10.69 and x = -0.56 after putting them in a calculator

answer = D

Answer these three questions for 100 points Question 1) Identifying the values a, b, and c is the fi

Mathematics

Step-by-step answer

P Answered by PhD

C, A, D

edit - sorry the title was wrong earlier

Step-by-step explanation:

Question 1

in the quadratic formula, the equation is in the format of ax^2 + bx + c

so rearrange this equation so all values are on one side

-6x^2 = -9x + 7

-6x^2 + 9x - 7 =0

so a = -6, b = 9, c = -7

answer = C

Question 2

note that all the values are already on one side for this, so repeat the process from question 1 where the equation is in the format of ax^2 + bx + c

the equation = −6x2 − 8x + 12 = 0

so a = -6, b = -8, c = 12

answer = A

Question 3

(see picture below for steps)

following the same process above, a = 4, b = 45, and c = 24, so plug these values in the quadratic equation shown in the picture below

so you get the answers x = -10.69 and x = -0.56 after putting them in a calculator

answer = D

Mathematics

Place the following steps in order to complete the square and solve for the quadratic equation, x squared -6x +7=0

Step-by-step answer

P Answered by Master

F,A,D,C,E,B

Step-by-step explanation:

I had this problem on algebra nation and got it right

Mathematics

Place the following steps in order to complete the square and solve for the quadratic equation, x squared -6x +7=0

Step-by-step answer

P Answered by Master

F,A,D,C,E,B

Step-by-step explanation:

I had this problem on algebra nation and got it right

Mathematics

21:20 In which step did Yvonne first make an error? Yvonne is solving the quadratic equation 6x2 + 24x + 7 = 0 by completing the square. Her first four steps are shown in the table. Yvonne s Work Step 1 Step 2 Step 3 Step 4 Step 1 Step 2 6x² +24x+7-0 6x² +24x - 7 6(x²+4x) -7 6(x²+4x+4) - 3+24 6(x+2)²-27 Step 3 Step 4 Mark this and return Save and Exit Next Submit

Step-by-step answer

P Answered by PhD

Step 2

Step-by-step explanation:

Given the quadratic equation 6x² + 24x + 7 = 0, the following steps must be followed when finding the roots using the completing the square method.

Step 1: Subtract 7 from both sides

6x² + 24x + 7 - 7= 0 -7

6x² + 24x = -7

Step 2: divide through by the coefficient of x²

6x²/6 + 24x/6 = -7/6

x² + 4x = -7/6

Step 3: Add half of the coefficient of x (i.e 4/2 = 2) to both sides of the equation to complete the square of the equation x² + 4x.

x² + 4x + 2= -7/6 + 2

(x+2)² = -7/6 + 2

(x+2)² = 5/6

Step 4: taking the square root of both sides

√(x+2)² = √5/6

x+2 = ±√5/6

x = -2±√5/6

x = -2+√5/6 and -2-√5/6

Based on the conclusion above, it can be seen that Yvonne made the first error in step 2. Yvonne suppose to divide through by the coefficient of x² (i.e 6)

Mathematics

Step-by-step answer

P Answered by PhD

Step 2

Step-by-step explanation:

Given the quadratic equation 6x² + 24x + 7 = 0, the following steps must be followed when finding the roots using the completing the square method.

Step 1: Subtract 7 from both sides

6x² + 24x + 7 - 7= 0 -7

6x² + 24x = -7

Step 2: divide through by the coefficient of x²

6x²/6 + 24x/6 = -7/6

x² + 4x = -7/6

Step 3: Add half of the coefficient of x (i.e 4/2 = 2) to both sides of the equation to complete the square of the equation x² + 4x.

x² + 4x + 2= -7/6 + 2

(x+2)² = -7/6 + 2

(x+2)² = 5/6

Step 4: taking the square root of both sides

√(x+2)² = √5/6

x+2 = ±√5/6

x = -2±√5/6

x = -2+√5/6 and -2-√5/6

Based on the conclusion above, it can be seen that Yvonne made the first error in step 2. Yvonne suppose to divide through by the coefficient of x² (i.e 6)

free Ask question

Today we have helped

380 students

just now

English