1.
You are right, answer D.
2.
First spin = 3 possible outcomes
Second spin = 3 possible outcomes
Third spin = 3 possible outcomes
so there will be 3*3*3 = 27 possible outcomes.
Answer D.
3.
Not 1 on the first spinner (so 2 or 3) = 2 possible outcomes
4 on the second spinner = 1 possible outcome
so there will be 2*1 = 2 possible outcomes.
Answer A.
4.
Answer A. (A six-sided number cube is rolled and a coin is flipped.)
and
Answer B. (Two spinners are spun at the same time.)
5.
First we have 10 slips of paper and there are 3 slips with number that is a multiple of 3 (3, 6 and 9). So:
P(multiple of 3) = 3/10
Now, we have only 9 slips and there are 2 with number that is multiple of 4 (4 and 8) so:
P(multiple of 4) = 2/9
And finally:
P(multiple of 3 and then a multiple of 4) = P(multiple of 3) * P(multiple of 4) =
=3/10 * 2/9 = 1/15
Answer A.
6.
We have 8 possible outcomes but only 4 even (2, 4, 6 and 8), so
P(even number on the first spin) = 4/8 = 1/2
The second spin is the same as the first one
P(even number on the second spin) = 4/8 = 1/2
And
P(even and even) = P(first even) * P(second even) = 1/2 * 1/2 = 1/4
Answer A.
7.
∩ means AND
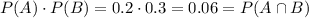
so P(A)*P(B) = P(A and B)
A and B are independent.
8.
Let B - like brownies and C - like cupcakes
From the table we know, that (total number):
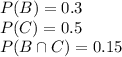
Calculete:
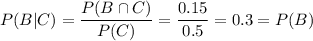
and
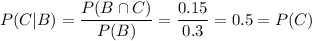
So P(B|C) = P(B) and P(C|B) = P(C) and B, C are independent.
Answer A.
9.
Answer A.
10.
Let G₁ - first ball is green and G₂ - second ball is green. We know that:
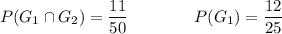
so:
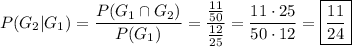
Answer B.
11.
All possible outcomes = 8
Number less than 4 = {1, 2, 3}
Multiple of 4 = {4, 8}
There is "number less than 4 OR a multiple of 4", so we take all numbers from both sets = {1, 2, 3, 4, 8} (5 outcomes)
P(less than 4 or a multiple of 4) = 5/8
Answer B.
12.
All possible outcomes = 10
Odd number = {1, 3, 5, 7, 9}
Number greater than 4 = {5, 6, 7, 8, 9, 10}
There is "an odd number AND a number greater than 4" so we take only numbers that are in both sets = {5, 7, 9} (3 outcomes)
P(an odd number and a number greater than 4) = 3/10
Answer C.