Suppose there are 4 defective batteries in a drawer with 10 batteries in it. A sample of 3 is taken at random without replacement. Let X denote the number of defective batteries in the sample. Find the probability that the sample contains a) Exactly one defective battery b) at most one defective battery. c) at least one defective battery.

a.) 0.5

b.) 0.66

c.) 0.83

Step-by-step explanation:

As given,

Total Number of Batteries in the drawer = 10

Total Number of defective Batteries in the drawer = 4

⇒Total Number of non - defective Batteries in the drawer = 10 - 4 = 6

Now,

As, a sample of 3 is taken at random without replacement.

a.)

Getting exactly one defective battery means -

1 - from defective battery

2 - from non-defective battery

So,

Getting exactly 1 defective battery = ⁴C₁ × ⁶C₂ =   ×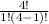

                                                                            = ×

                                                                            = ×

                                                                            = ×

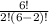
                                                                            = × = 60

Total Number of possibility = ¹⁰C₃ =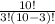

                                                        =

                                                        =

                                                        =

                                                        = 120

So, probability =

b.)

at most one defective battery :

⇒either the defective battery is 1 or 0

If the defective battery is 1 , then 2 non defective

Possibility  = ⁴C₁ × ⁶C₂ = 60

If the defective battery is 0 , then 3 non defective

Possibility   = ⁴C₀ × ⁶C₃

                   =   ×

                   = ×

                   = 1 ×

                   = 1×

                   = 1 × 20 = 20

getting at most 1 defective battery = 60 + 20 = 80

Probability =

c.)

at least one defective battery :

⇒either the defective battery is 1 or 2 or 3

If the defective battery is 1 , then 2 non defective

Possibility  = ⁴C₁ × ⁶C₂ = 60

If the defective battery is 2 , then 1 non defective

Possibility   = ⁴C₂ × ⁶C₁

                   =   ×

                   = ×

                   = ×

                   = ×

                   = 6 × 6 = 36

If the defective battery is 3 , then 0 non defective

Possibility   = ⁴C₃ × ⁶C₀

                   =   ×

                   = ×

                   = × 1

                   = 4×1 = 4

getting at most 1 defective battery = 60 + 36 + 4 = 100

Probability =

The answer is in the image 

SI=(P*R*T)/100

P=2000

R=1.5

T=6

SI=(2000*1.5*6)/100

=(2000*9)/100

=180

Neil will earn interest of 180

For 1 flavor there are 9 topping

Therefore, for 5 different flavors there will be 5*9 choices

No of choices= 5*9

=45 

The answer is in the image 

The answer is in the image 

For every 8 cars there are 7 trucks

Therefore,

Cars:Truck=8:7

Answer is B)8:7

F=ma

where F=force

m=mass

a=acceleration

Here,

F=4300

a=3.3m/s2

m=F/a

    =4300/3.3

    =1303.03kg

F=ma

where F=force

m=mass

a=acceleration

Here,

F=4300

a=3.3m/s2

m=F/a

    =4300/3.3

    =1303.03kg

Approximately it is aqual to 1300kg

The answer is in the image