A ramp has an angle of inclination of 20 degrees., №17886644, 06.08.2020 20:49

Mathematics

A ramp has an angle of inclination of 20 degrees. it has a vertical height of 1.8 m. what is the length, l metres, of the ramp?

Step-by-step answer

P Answered by PhD

9

x = 5.26 m

Step-by-step explanation:

Given that,

The angle of inclination = 20°

The vertical height of the ramp, h = 1.8 m

We need to find the length of the ramp. Let it is x.

We can find it using trigonometry. So,

$\sin\theta=\dfrac{P}{H}$

We have,

P = 1.8 m, H = x

$\sin20=\dfrac{1.8}{x}\\\\x=\dfrac{1.8}{\sin20}\\\\x=5.26\ m$

So, the length of the ramp is 5.26 m.

Mathematics

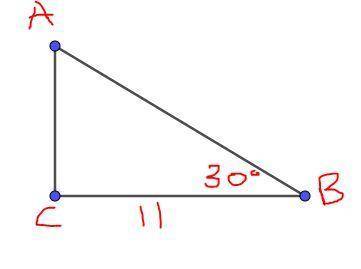
1. in abc, c is a right angle and bc= 11. if the measure of angle b= 30degrees, find ac. a) (11sqrt3)/3 b) 3sqrt/11 c)11/2 d)11sqrt3/2 2.which of the following angles has a reference angle of pi/8? a)-51pi/8 b)11pi/8 c)-33pi/8 d)27pi/8 3.your town’s public library is building a new wheelchair ramp to its entrance. by law, the maximum angle of incline for the ramp is 4.76 degrees. the ramp will have a vertical ride of 2.5 ft. what is the shortest horizontal distance that the ramp can span? a)11.9ft b)30.0ft c)4.3ft d)19.1ft 4. find the exact value

Step-by-step answer

P Answered by Specialist

1. The given triangle ABC, has a right angle at C, BC=11, and 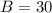$B=30\degree$

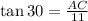
$\tan 30\degree=\frac{AC}{11}$

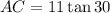
$AC=11\tan 30\degree$

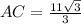
$AC=\frac{11\sqrt{3}}{3}$

Ans: A

2. The reference angle is the angle the terminal side makes with x-axis.

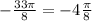
$-\frac{33\pi}{8}=-4\frac{\pi}{8}$

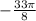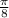This implies that, $-\frac{33\pi}{8}$ has a reference angle of $\frac{\pi}{8}$ .

Ans: C

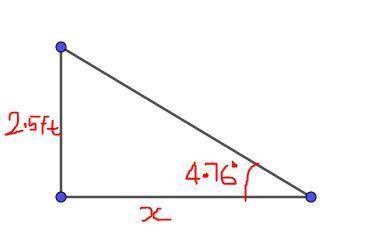
3. Let x be the shortest distance the ramp can span.

From the diagram; 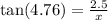$\tan (4.76\degree)=\frac{2.5}{x}$

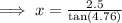
$\implies x=\frac{2.5}{\tan (4.76\degree)}$

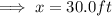
$\implies x=30.0ft$

Ans:B

4. Use the Pythagorean identity: 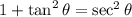$1+\tan ^2 \theta=\sec^2 \theta$ .

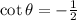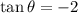
If $\cot \theta=-\frac{1}{2}$ ,then $\tan \theta=-2$

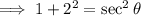
$\implies 1+2^2=\sec^2 \theta$

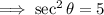
$\implies \sec^2 \theta=5$

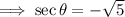$\implies \sec \theta=-\sqrt{5}$ , In QII, the secant ratio is negative.

Ans:C

5. We have 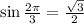$\sin \frac{2\pi}{3}=\frac{\sqrt{3} }{2}$

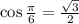
$\cos \frac{\pi}{6}=\frac{\sqrt{3} }{2}$

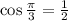
$\cos \frac{\pi}{3}=\frac{1}{2}$

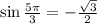
$\sin \frac{5\pi}{3}=-\frac{\sqrt{3} }{2}$

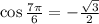
$\cos \frac{7\pi}{6}=-\frac{\sqrt{3} }{2}$

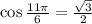
$\cos \frac{11\pi}{6}=\frac{\sqrt{3} }{2}$

Ans:A and D

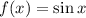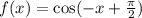6. The given function that is equivalent to $f(x)=\sin x$ is $f(x)=\cos (-x+\frac{\pi}{2})$ .

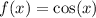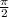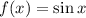When we reflect the graph of $f(x)=\cos (x)$ in the y-axis and shift it to the left by $\frac{\pi}{2}$ units, it coincides with graph of $f(x)=\sin x$ .

Ans:C

7. The function 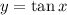$y=\tan x$ is a one-to-one function on the interval $[-\frac{\pi}{2},\frac{\pi}{2}]$

When we restrict the domain of 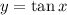$y=\tan x$ on $[-\frac{\pi}{2},\frac{\pi}{2}]$ it becomes an invertible function.

Ans: C

8. The given function is 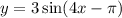$y=3\sin(4x-\pi)$

The horizontal shift is given by 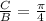$\frac{C}{B}=\frac{\pi}{4}$

The direction of the shift is to the right.

Ans:D

9. 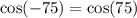$\cos(-75\degree)=\cos(75\degree)$ by the symmetric property of even functions.

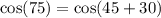
$\cos(75\degree)=\cos(45\degree+30\degree)$

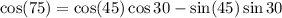
$\cos(75\degree)=\cos(45\degree) \cos30\degree-\sin(45\degree) \sin30\degree$

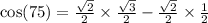
$\cos(75\degree)=\frac{\sqrt{2} }{2} \times \frac{\sqrt{3} }{2} -\frac{\sqrt{2} }{2} \times \frac{1}{2}$

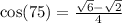
$\cos(75\degree)=\frac{\sqrt{6}-\sqrt{2}}{4}$

Ans: B

10. Recall the cosine rule: 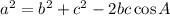$a^2=b^2+c^2-2bc\cos A$

Let the angle measure opposite to the longest side be A, then a=19,b=17, and c=15.

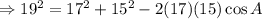
$\Rightarrow 19^2=17^2+15^2-2(17)(15)\cos A$

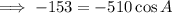
$\implies -153=-510\cos A$

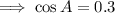
$\implies \cos A=0.3$

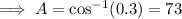
$\implies A=\cos^{-1}(0.3)=73\degree$

Ans:B

11. We want to solve 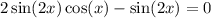$2\sin(2x)\cos(x)-\sin(2x)=0$ on the interval;

$[-\frac{\pi}{2},\frac{\pi}{2}]$

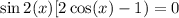
Factor: $\sin2(x)[2\cos(x)-1)=0$

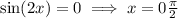
Either $\sin(2x)=0 \implies x=0\frac{\pi}{2}$

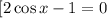Or $[2\cos x-1=0$ This means that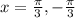 $x=\frac{\pi}{3},-\frac{\pi}{3}$

Therefore required solution is 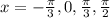$x=-\frac{\pi}{3},0,\frac{\pi}{3},\frac{\pi}{2}$

Ans:D

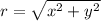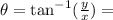
12. Use the relation: $r=\sqrt{x^2+y^2}$ and $\theta=\tan^{-1}(\frac{y}{x})=$

The given rectangular coordinate is (1,-2)

This implies that: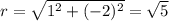 $r=\sqrt{1^2+(-2)^2}=\sqrt{5}$

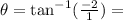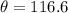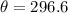
$\theta=\tan^{-1}(\frac{-2}{1})=$ This means $\theta=116.6$ or $\theta=296.6$

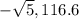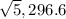
The polar forms are: $-\sqrt{5},116.6$ and $\sqrt{5},296.6$

Ans: B and C

13. The polar equation that represents an ellipse is

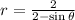$r=\frac{2}{2-\sin \theta}$ .

When written in standard form; 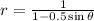$r=\frac{1}{1-0.5\sin \theta}$ .

The eccentricity is 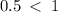$0.5\:$ .

Therefore the 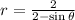$r=\frac{2}{2-\sin \theta}$ is an ellipse.

Ans: B

14. The DeMoivre’s Theorem states that;

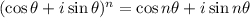
$(\cos \theta+i\sin \theta)^n=\cos n\theta+i\sin n\theta$

This implies that:

$[2(\cos \frac{\pi}{9}+i\sin \frac{\pi}{9})]^3=2^3\cos 3\times \frac{\pi}{9}+i\sin 3\times \frac{\pi}{9})$

$[2(\cos \frac{\pi}{9}+i\sin \frac{\pi}{9})]^3=8(frac{2}{2})+i8(\frac{\sqrt{3}}{2})=4+4\sqrt{3}i$

Ans: A

15. Let the initial point be (x,y), Then 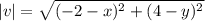$|v|=\sqrt{(-2-x)^2+(4-y)^2}$ .

If x=-8, and y=-4.

Then, 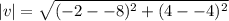$|v|=\sqrt{(-2--8)^2+(4--4)^2}$ .

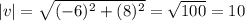$|v|=\sqrt{(-6)^2+(8)^2}=\sqrt{100}=10$ .

Ans: B

16. We find the dot product to see if it is zero.

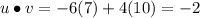
$u\bullet v=-6(7)+4(10)=-2$

Since the dot product is not zero the vectors are not orthogonal

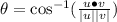
$\theta=\cos ^{-1}(\frac{u\bullet v}{|u||v|})$

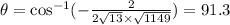
$\theta=\cos ^{-1}(-\frac{2}{2\sqrt{13}\times \sqrt{1149} }) =91.3\degree$

Ans:B

17. Given v=5i+4j, w=2i-3j.

u=v+w

Add corresponding components

This implies u=(5i+4j)+(2i-3j)

u=(5i+2i+4j-3j)

u=7i+j

Ans:B

See attachment.

1. in abc, c is a right angle and bc= 11. if the measure of angle b= 30degrees, find ac. a) (11sqrt3

Physics

A stunt cyclist needs to make a calculation for an upcoming cycle jump. The cyclist is traveling 100 ft/sec toward an inclined ramp which ends 10 feet above a level landing zone. Assume the cyclist maintains a constant speed up the ramp and the ramp is inclined Ao (degrees) above horizontal. With the pictured imposed coordinate system, the parametric equations of the cyclist will be: x(t) = 100t cos(A) y(t) = –16t2 + 100t sin(A) + 10. Calculate the horizontal velocity of the cyclist at time t; this is the function x (t) = What is the horizontal

Step-by-step answer

P Answered by Master

Explanation:

The parametric equations of the cyclist are:

$x(t)=100tcos(A)\\\\y(t)=-16t^2+100tsin(A)+10$ (1)

A) The horizontal velocity is the derivative of x(t), in time:

x'(t)=100cos(A)

B) For A=20° the horizontal velocity is:

$v_x=x'(t)=100cos(20\°)=93.9692ft/s$

For A=45°:

$v_x=100cos(45\°)=70.7106ft/s$

C) To find the time in which the vertical velocity is zero you first obtain the derivative of, in time:

v_y=y'(t)=-32t+100sin(A)+10

Next, you equal the vertical velocity to zero and solve for time t:

$-32t+100sin(A)+10=0\\\\t=\frac{100sin(A)+10}{32}$

D) The maximum height is reached when the derivative of y (height) is zero. You use the previous value of t in the equation (1), equals y to 35. Next, you solve for t:

$y=35\\\\-16(\frac{100sin(A)+10}{32})^2+100(\frac{10sin(A)+10}{32})sinA+10=35\\\\-\frac{16}{1024}(10000sin^2A+2000sinA+100)+31.25sin^2A+31.25sinA+10=35\\\\-156.25sin^2A-31.25sinA-1.5625+31.25sin^2A+31.25sinA+10=35\\\\-125sin^2A-26.5625=0$

Physics

A stunt cyclist needs to make a calculation for an upcoming cycle jump. The cyclist is traveling 100 ft/sec toward an inclined ramp which ends 10 feet above a level landing zone. Assume the cyclist maintains a constant speed up the ramp and the ramp is inclined Ao (degrees) above horizontal. With the pictured imposed coordinate system, the parametric equations of the cyclist will be: x(t) = 100t cos(A) y(t) = –16t2 + 100t sin(A) + 10. Calculate the horizontal velocity of the cyclist at time t; this is the function x (t) = What is the horizontal

Step-by-step answer

P Answered by Specialist

Explanation:

The parametric equations of the cyclist are:

$x(t)=100tcos(A)\\\\y(t)=-16t^2+100tsin(A)+10$ (1)

A) The horizontal velocity is the derivative of x(t), in time:

x'(t)=100cos(A)

B) For A=20° the horizontal velocity is:

$v_x=x'(t)=100cos(20\°)=93.9692ft/s$

For A=45°:

$v_x=100cos(45\°)=70.7106ft/s$

C) To find the time in which the vertical velocity is zero you first obtain the derivative of, in time:

v_y=y'(t)=-32t+100sin(A)+10

Next, you equal the vertical velocity to zero and solve for time t:

$-32t+100sin(A)+10=0\\\\t=\frac{100sin(A)+10}{32}$

D) The maximum height is reached when the derivative of y (height) is zero. You use the previous value of t in the equation (1), equals y to 35. Next, you solve for t:

$y=35\\\\-16(\frac{100sin(A)+10}{32})^2+100(\frac{10sin(A)+10}{32})sinA+10=35\\\\-\frac{16}{1024}(10000sin^2A+2000sinA+100)+31.25sin^2A+31.25sinA+10=35\\\\-156.25sin^2A-31.25sinA-1.5625+31.25sin^2A+31.25sinA+10=35\\\\-125sin^2A-26.5625=0$

Mathematics

You can buy jars of the same jam in 2 sizes large jar:440g for £1.54 small jar:340g for £1.26 By considering the price per gram, work out which jar is the best value for money. Working must be shown

Step-by-step answer

P Answered by PhD

Answer: 440 grams for 1.54 is the better value
Explanation:
Take the price and divide by the number of grams
1.54 / 440 =0.0035 per gram
1.26 / 340 =0.003705882 per gram
0.0035 per gram < 0.003705882 per gram

Mathematics

Anthony received $150 for his birthday this year. This was $10 less than half the amount he received last year. How much money did Anthony receive for his birthday last year?

Step-by-step answer

P Answered by PhD

The answer is in the image

Mathematics

A 4300-N force from a car s engines produces an acceleration of 3.3 m/s2. What is the mass of the car? A. 4300 kg B. 1300 kg C. 14,000 kg D. 390 kg

Step-by-step answer

P Answered by PhD

F=ma

where F=force

m=mass

a=acceleration

Here,

F=4300

a=3.3m/s2

m=F/a

=4300/3.3

=1303.03kg

Approximately it is aqual to 1300kg

Mathematics

Thomas got a haircut from the barber. If the haircut costs $32 and he wants to leave a 18% tip, how much will he pay in total?

Step-by-step answer

P Answered by PhD

Here,

tip=18%of $32

tip=(18/100)*32

=0.18*32

=$5.76

Total payment=32+5.76=$37.76

Mathematics

Mathematics, 26.03.2020 20:52, mohammadhosseinkarim David is building wooden picture frames. Each frame requires 3/4 feet of wood. If David started with 12 feet of wood and now has 6 feet of wood remaining, how many pictures frames has he built?

Step-by-step answer

P Answered by PhD

The wood before starting =12 feet

Left wood=6 feet

Wood used till now=12-6=6 feet

Picture frame built till now= 6/(3/4)

=8 pieces

Therefore, till now 8 pieces have been made.

Mathematics

Of the 420 students enrolled in basic math, only 30% are first-year students. How many are first-year students? How many are not?

Step-by-step answer

P Answered by PhD

30% of 420 are first year students

first year students = (30/100 )*420

=126 students

Student who are not in first year = 420-126

=294 students

A ramp has an angle of inclination of 20 degrees. it has a vertical height of 1.8 m. what is the length, l metres, of the ramp?

Step-by-step answer

Faq

Try asking the Studen AI a question.