A maintenance technician sights the top of a telephone pole at a 25° angle of elevation as shown. Technician Telephone Pole Determine the horizontal distance between the technician and the base of the telephone pole to the nearest tenth of a foot. Enter your answer in the box.

Step-by-step explanation:

Given

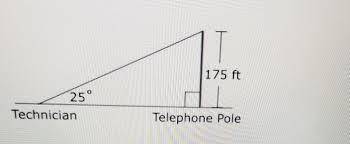
See attachment for illustration

Required

Determine the horizontal distance

The horizontal distance is the distance between the technician and the base of the pole.

Represent this with x.

The relationship between x, 175ft and 25 degrees is represented as:

--- i.e. tan formula

Multiply both sides by x

Make x the subject

--- approximated

The distance is approximately 375.3ft

The answer is in the image 

Cost of 7 gallons=$24.50

Cost of 1 gallon=24.50/7=3.5

Cost of 15 gallons=15*3.5=52.5

Cost of 15 gallons will be $52.5

The answer is in the image 

The answer is in the image 

The answer is in the image 

The answer is in the image 

The answer is in the image 

Salesperson will make 6% of 1800

=(6/100)*1800

=108

Salesperson will make $108 in $1800 sales