Mathematics: If x ≠ 0 then what is x^0?

Step-by-step explanation: because if you are dong it 0 times it would be just x (make sense?)...

If x ≠ 0 then what is x^0?, №17887095, 15.09.2022 03:11

Mathematics

Write an equation for the translation of y = |x| down 0.75 units. y = |x – 0.75| y = |x| + 0.75 y = |x| – 0.75 y = |x + 0.75|

Step-by-step answer

P Answered by Master

7

Y=|x|-0.75 because subtracting will shift the problem down

Mathematics

Write an equation for the translation of y = |x| down 0.75 units. y = |x – 0.75| y = |x| + 0.75 y = |x| – 0.75 y = |x + 0.75|

Step-by-step answer

P Answered by Specialist

7

Y=|x|-0.75 because subtracting will shift the problem down

Mathematics

Solve the lp problem. if no optimal solution exists, indicate whether the feasible region is empty or the objective function is unbounded. hint [see example 1.] (enter empty if the region is empty. enter unbounded if the function is unbounded.) maximize p = x − 2y subject to x + 4y ≤ 9 x − 5y ≤ 0 6x − 3y ≥ 0 x ≥ 0, y ≥ 0.

Step-by-step answer

P Answered by PhD

1

A graphical solution shows the objective function is maximized for (x, y) = (5, 1). The corresponding value of p is
p = 3
Solve the lp problem. if no optimal solution exists, indicate whether the feasible region is empty o

Mathematics

Solve the lp problem. if no optimal solution exists, indicate whether the feasible region is empty or the objective function is unbounded. hint [see example 1.] (enter empty if the region is empty. enter unbounded if the function is unbounded.) maximize p = x − 2y subject to x + 4y ≤ 9 x − 5y ≤ 0 6x − 3y ≥ 0 x ≥ 0, y ≥ 0.

Step-by-step answer

P Answered by PhD

1

A graphical solution shows the objective function is maximized for (x, y) = (5, 1). The corresponding value of p is
p = 3
Solve the lp problem. if no optimal solution exists, indicate whether the feasible region is empty o

Chemistry

If the reaction is carried out in a 22.4 L container, which initial amounts of X and Y will result in the formation of solid XY? If the reaction is carried out in a 22.4 container, which initial amounts of and will result in the formation of solid ? 2.0 mol X; 2.0 molY 6 mol X; 0.6 molY 1 mol X; 1 molY none of the above

Step-by-step answer

P Answered by Specialist

This is an incomplete question, here is the complete question.

The solid XY decomposes into gaseous X and Y:

$XY(s)\rightleftharpoons X(g)+Y(g)$ Kp = 4.1 (at 0°C)

If the reaction is carried out in a 22.4 L container, which initial amounts of X and Y will result in the formation of solid XY?

a) 2.0 mol X; 2.0 mol Y

b) 6 mol X; 0.6 mol Y

c) 1 mol X; 1 mol Y

d) None of the above

Answer : The correct option is, (D) None of the above

Explanation :

Reaction quotient (Q) : It is defined as the measurement of the relative amounts of products and reactants present during a reaction at a particular time.

The given balanced chemical reaction is,

$XY(s)\rightleftharpoons X(g)+Y(g)$

The expression for reaction quotient will be :

Q = [X] [Y]

In this expression, only gaseous or aqueous states are includes and pure liquid or solid states are omitted.

The given equilibrium constant value is, K_p=4.1

Equilibrium constant : It is defined as the equilibrium constant. It is defined as the ratio of concentration of products to the concentration of reactants.

If the initial amount of X and Y to form XY then the product of their product must be greater than Kp.

Now we have to calculate the product of partial pressure.

PV = nRT

$P=\frac{nRT}{V}$

Moles of X Moles of Y Pressure of X Pressure of Y Q

2.0 2.0 2.00 2.00 4.00

6 0.6 6.00 0.6 3.6

1 1 1.00 1.00 1.00

There are 3 conditions:

When QK_c that means product > reactant. So, the reaction is reactant favored.

When that means reactant > product. So, the reaction is product favored.

When Q=K_c that means product = reactant. So, the reaction is in equilibrium.

From the above we conclude that, in all the three options that means product < reactant. So, the reaction is product favored that means reaction must shift to the product (right) to be in equilibrium. That means the reaction will not move to the left to form XY.

Hence, the correct option is, (D)

Mathematics

What statement makes the open sentence 1.4=7x true? x=5.6 x=2.0 x=0.5 x=0.2

Step-by-step answer

P Answered by Master

7

To solve this, divide 7 and 1.4

1.4/7 = 0.2

Mathematics

Use the Laplace transform to solve the given system of differential equations. d2x dt2 + x âˆ’ y = 0 d2y dt2 + y âˆ’ x = 0 x(0) = 0, x (0) = âˆ’6, y(0) = 0, y (0) = 1

Step-by-step answer

P Answered by Specialist

I'm going to assume that "âˆ’" is supposed to be some kind of minus character, so that the given system of DEs is supposed to be

$\begin{cases}\dfrac{\mathrm d^2x}{\mathrm dt^2} + x - y = 0 \\ \dfrac{\mathrm d^2y}{\mathrm dt^2} + y - x = 0 \\ x(0) = 0, x'(0) = -6, y(0) = 0, y'(0) = 1\end{cases}$

Take the Laplace transform of both sides of both equations. Recall the transform for a second-order derivative,

$L_s\left\{\dfrac{\mathrm d^2f(t)}{\mathrm dt^2}\right\} = s^2 F(s) - sf(0) - f'(0)$

where F(s) denotes the transform of f(t). You end up with

$\begin{cases}s^2X(s)-sx(0)-x'(0) + X(s) - Y(s) = 0 \\ s^2Y(s) - sy(0) - y'(0) + Y(s) - X(s) = 0\end{cases} \\\\ \begin{cases}(s^2+1)X(s) - Y(s) = -6 \\ (s^2+1)Y(s) - X(s) = 1\end{cases}$

and solving for X(s) and Y(s) (nothing tricky here, just two linear equations) gives

$X(s) = -\dfrac{6s^2+5}{s^2(s^2+2)} \text{ and } Y(s) = \dfrac{s^2-5}{s^2(s^2+2)}$

Now solve for x(t) and y(t) by computing the inverse transforms. To start, split up both X(s) and Y(s) into partial fractions.

• Solving for x(t) :

$-\dfrac{6s^2+5}{s^2(s^2+2)} = \dfrac as + \dfrac b{s^2} + \dfrac{cs+d}{s^2+2} \\\\ -6s^2-5 = as(s^2+2) + b(s^2+2) + (cs+d)s^2 \\\\ -6s^2-5 = (a+c)s^3 + (b+d)s^2 + 2as + 2b \\\\ \implies \begin{cases}a+c=0\\b+d=-6\\2a=0\\2b=-5\end{cases} \implies a=c=0, b=-\dfrac52, d=-\dfrac72$

$\implies X(s) = -\dfrac5{2s^2} - \dfrac7{2(s^2+2)}$

Taking the inverse transform, you get

$L^{-1}_t\left\{X(s)\right\} = -\dfrac52 L^{-1}_t\left\{\dfrac{1!}{s^{1+1}}\right\} - \dfrac7{2\sqrt2} L^{-1}_t\left\{\dfrac{\sqrt2}{s^2+(\sqrt2)^2}\right\} \\\\ \implies \boxed{x(t) = -\dfrac52 t - \dfrac7{2\sqrt2}\sin(\sqrt2\,t)}$

• Solving for y(t) :

$\dfrac{s^2-5}{s^2(s^2+2)} = \dfrac as + \dfrac b{s^2} + \dfrac{cs+d}{s^2+2} \\\\ s^2 - 5 = as(s^2+2) + b(s^2+2) + (cs+d)s^2 \\\\ s^2 - 5 = (a+c)s^3 + (b+d)s^2 + 2as + 2b \\\\ \implies \begin{cases}a+c=0\\b+d=1\\2a=0\\2b=-5\end{cases} \implies a=c=0, b=-\dfrac52, d=\dfrac72$

$\implies Y(s) = -\dfrac5{2s^2} + \dfrac7{2(s^2+2)}$

Inverse transform:

$L^{-1}_t\left\{Y(s)\right\} = -\dfrac52 L^{-1}_t\left\{\dfrac{1!}{s^{1+1}}\right\} + \dfrac7{2\sqrt2} L^{-1}_t\left\{\dfrac{\sqrt 2}{s^2+(\sqrt2)^2}\right\} \\\\ \implies \boxed{y(t) = -\dfrac52 t + \dfrac7{\sqrt2} \sin(\sqrt2\,t)}$

Chemistry

If the reaction is carried out in a 22.4 L container, which initial amounts of X and Y will result in the formation of solid XY? If the reaction is carried out in a 22.4 container, which initial amounts of and will result in the formation of solid ? 2.0 mol X; 2.0 molY 6 mol X; 0.6 molY 1 mol X; 1 molY none of the above

Step-by-step answer

P Answered by Master

This is an incomplete question, here is the complete question.

The solid XY decomposes into gaseous X and Y:

$XY(s)\rightleftharpoons X(g)+Y(g)$ Kp = 4.1 (at 0°C)

If the reaction is carried out in a 22.4 L container, which initial amounts of X and Y will result in the formation of solid XY?

a) 2.0 mol X; 2.0 mol Y

b) 6 mol X; 0.6 mol Y

c) 1 mol X; 1 mol Y

d) None of the above

Answer : The correct option is, (D) None of the above

Explanation :

Reaction quotient (Q) : It is defined as the measurement of the relative amounts of products and reactants present during a reaction at a particular time.

The given balanced chemical reaction is,

$XY(s)\rightleftharpoons X(g)+Y(g)$

The expression for reaction quotient will be :

Q = [X] [Y]

In this expression, only gaseous or aqueous states are includes and pure liquid or solid states are omitted.

The given equilibrium constant value is, K_p=4.1

Equilibrium constant : It is defined as the equilibrium constant. It is defined as the ratio of concentration of products to the concentration of reactants.

If the initial amount of X and Y to form XY then the product of their product must be greater than Kp.

Now we have to calculate the product of partial pressure.

PV = nRT

$P=\frac{nRT}{V}$

Moles of X Moles of Y Pressure of X Pressure of Y Q

2.0 2.0 2.00 2.00 4.00

6 0.6 6.00 0.6 3.6

1 1 1.00 1.00 1.00

There are 3 conditions:

When QK_c that means product > reactant. So, the reaction is reactant favored.

When that means reactant > product. So, the reaction is product favored.

When Q=K_c that means product = reactant. So, the reaction is in equilibrium.

From the above we conclude that, in all the three options that means product < reactant. So, the reaction is product favored that means reaction must shift to the product (right) to be in equilibrium. That means the reaction will not move to the left to form XY.

Hence, the correct option is, (D)

Mathematics

What statement makes the open sentence 1.4=7x true? x=5.6 x=2.0 x=0.5 x=0.2

Step-by-step answer

P Answered by Specialist

7

To solve this, divide 7 and 1.4

1.4/7 = 0.2

Mathematics

Asap, good answers get brainliest +50 wrong answers get reported. 9.06 1. find the derivative of f(x) = -4x2 + 11x at x = 10. a) -19.5 b) -69 c) 30 d) -300 2. find the derivative of f(x) = 8x + 4 at x = 9. a) 0 b) 4 c) 8 d) 9 3. find the derivative of f(x) = 4 divided by x at x = 2. a) -4 b) -1 c) 1 d) 4 4. find the derivative of f(x) = negative 9 divided by x at x = -4. a) 4 divided by 9 b) 16 divided by 9 c) 9 divided by 16 d) 9 divided by 4 5. find the limit of the function by using direct substitution. limit as x approaches zero of quantity

Step-by-step answer

P Answered by PhD

30

(1) Ans: Option (B) -69

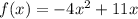
Given function: f(x) = -4x^2 + 11x

The derivative of f(x) with respect to x is:

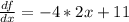
$\frac{df}{dx} = -4 * 2x + 11$ --- (1)

Plug the value of x = 10 in (1)

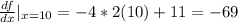
(1) => $\frac{df}{dx} |_{x=10} = -4 * 2(10) + 11 = -69$

Hence the correct answer is Option (B) -69

(2) Ans: Option (C) 8

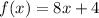
Given function: f(x) = 8x + 4

The derivative of f(x) with respect to x is:

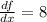
$\frac{df}{dx} = 8$ --- (1)

Plug the value of x = 9 in (1)

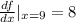
(1) => $\frac{df}{dx} |_{x=9} = 8$

Hence the correct answer is Option (C) 8

(3) Ans: Option (B) -1.

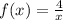
Given function: $f(x) = \frac{4}{x}
$

The derivative of f(x) with respect to x is:
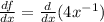
$\frac{df}{dx} = \frac{d}{dx}(4x^{-1})$
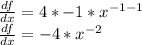
$\frac{df}{dx} = 4 * -1 * x^{-1 -1} \\ 
\frac{df}{dx} = -4 * x^{-2}$

At x = 2:
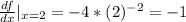
$\frac{df}{dx} |_{x=2} = -4 * (2)^{-2} = -1$

Hence the correct answer is Option (B) -1.

(4) Ans: Option (C) 9 divided by 16.
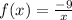
Given function: $f(x) = \frac{-9}{x}$

The derivative of f(x) with respect to x is:
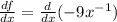
$\frac{df}{dx} = \frac{d}{dx}(-9x^{-1})$
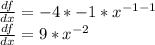
$\frac{df}{dx} = -4 * -1 * x^{-1 -1} \\ \frac{df}{dx} = 9 * x^{-2}$

At x = -4:
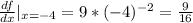
$\frac{df}{dx} |_{x=-4} = 9 * (-4)^{-2} = \frac{9}{16}$

Hence the correct answer is Option (C) 9 divided by 16.

(5) Ans: Option (D) 5

Given function:
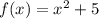
f(x) = x^2 + 5

Now apply the limit:
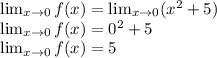
$\lim_{x \to 0} f(x) = \lim_{x \to 0} (x^2 + 5) \\
 \lim_{x \to 0} f(x) = 0^2 + 5\\
 \lim_{x \to 0} f(x) = 5$

The correct answer is Option (D) 5.

(6) Ans: Option (D) 27

Given function:
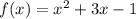
f(x) = x^2 + 3x - 1

Apply the limit:
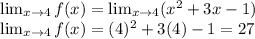
$\lim_{x \to 4} f(x) = \lim_{x \to 4} (x^2 + 3x - 1) \\
 \lim_{x \to 4} f(x) = (4)^2 + 3(4) -1 = 27$

The correct option is (D) 27

(7) Ans: Option (D) 8.

Given function:
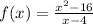
$f(x) = \frac{x^2 - 16}{x-4}$

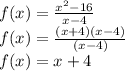
$f(x) = \frac{x^2 - 16}{x-4} \\
f(x) = \frac{(x+4)(x-4)}{(x-4)} \\
f(x) = x+4

$

Now apply limit:
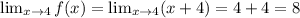
$\lim_{x \to 4} f(x) = \lim_{x \to 4} (x + 4) = 4+4 = 8$

The correct option is (D) 8.

(8) Ans: Option (A) Does not exist.

Given function:
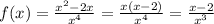
$f(x) = \frac{x^2 - 2x}{x^4} = \frac{x(x-2)}{x^4} = \frac{x-2}{x^3}$
Apply limit:
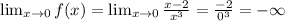
$\lim_{x \to 0} f(x) = \lim_{x \to 0} \frac{x-2}{x^3} = \frac{-2}{0^3} = -\infty$

The correct answer is (A) Does not exist.

(9),(10)
Please attach the graphs! Thanks! :)

(11) Ans: limit doesn't exist (Option C)
Given function:
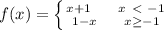
$f(x) = \left \{ {{x+1~~~~~x\ \textless \ -1} \atop {1-x~~~~~x\geq -1}} \right.$

If both sides are equal on applying limit then limit does exist.

Let check:
If x<-1: answer would be -1+1 = 0
If x≥-1: answer would be 1-(-1) =2

Since both are not equal, as 0≠2, hence limit doesn't exist (Option C).

(12) Ans: Option (B) 7.

Given function:
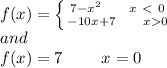
$f(x) = \left \{ {{7-x^2~~~~~x\ \textless \ 0} \atop {-10x+7~~~~~x\textgreater 0}} \right. \\
and \\
f(x) = 7~~~~~~~x=0



$

If all of above three are equal upon applying limit, then limit exists.

When x < 0 -> 7-(0)^2 = 7
When x = 0 -> 7
When x > 0 -> -10(0) + 7 = 7

ALL of the THREE must be equal. As they are equal. Hence the correct option is (B) 7.

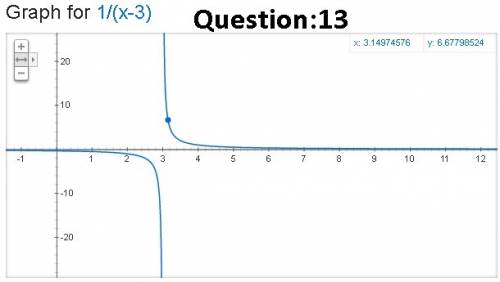
(13) Ans: -∞, x =3 (Option C)

Given function:
f(x) = 1/(x-3).
Table:
x f(x)=1/(x-3)
----------------------------------------
2.9 -10
2.99 -100
2.999 -1000
2.9999 -10000
3.0 -∞

Below the graph is attached! As you can see in the graph that at x=3, the curve approaches but NEVER exactly touches the x=3 line. Also the curve is in downward direction when you approach from the left. Hence, -∞, x =3 (Option C)

(14) Ans: Inst. velocity = -13

Given function:
s(t) = -1 -13t
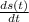
Instantaneous velocity = $\frac{ds(t)}{dt}$
Therefore,
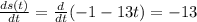
$\frac{ds(t)}{dt} = \frac{d}{dt} (-1-13t) = -13$

At t=8:
Inst. velocity = -13

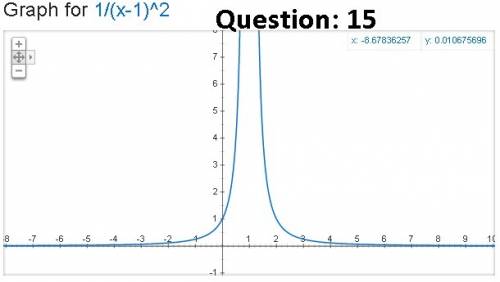
(15) Ans: +∞, x =1

Given function:
f(x) = 1/(x-1)^2
Table:
x f(x)= 1/(x-1)^2
----------------------------------
0.9 +100
0.99 +10000
0.999 +1000000
0.9999 +100000000
1.0 +∞

Below the graph is attached! As you can see in the graph that at x=1, the curve approaches but NEVER exactly touches the x=1 line. The curve is in upward direction if approached from left or right. Hence, the correct answer is: +∞, x =1

Asap, good answers get brainliest +50 wrong answers get reported. 9.06 1. find the derivative of f(

Asap, good answers get brainliest +50 wrong answers get reported. 9.06 1. find the derivative of f(

If x ≠ 0 then what is x^0?

Step-by-step answer

Faq

Try asking the Studen AI a question.