Given that a = ( − 6 7 ) and b = ( − 1 − 3 ), №17887505, 22.04.2023 11:39

Mathematics

Given that a = ( − 6 7 ) and b = ( − 1 − 3 ) . If a − b = ( x y ) , work out the values of x and y .

Step-by-step answer

P Answered by PhD

x = -5 , y = 10

Step-by-step explanation:

As given ,

a = ( x₁ , y₁ ) = ( -6, 7)

b = ( x₂ , y₂ ) = (-1, -3)

For a -b = ( x₁ - x₂ , y₁ - y₂ )

= ( -6 - (-1) , 7 - (-3) )

= ( -6 + 1 , 7 + 3 )

= ( -5 , 10 )

⇒ a - b = ( -5, 10 ) = ( x, y)

∴ we get

x = -5 , y = 10

Mathematics

Will get brainiest and points 1. write an equation that relates the number of triangles in the figure (n), to the perimeter of the figure (p) a. the equation for the perimeter is p = 5n + 7 b. the equation for the perimeter is p = 5n + 14 c. the equation for the perimeter is p = 7n + 10 d. the equation for the perimeter is p = 7n + 5 2. the table shows the relationship between the number of sports teams a person belongs to and the amount of free time the person has each week. number of sports teams | free time (hours) 0 46 1 39 2 32 3 25 is the

Step-by-step answer

P Answered by PhD

ANSWER TO QUESTION 1

Method 1: Observing a pattern.

Perimeter is the distance around the triangle.

For the first triangle, the perimeter is

P = 7 + 7 + 5

Let us write the sum of the 7s and 5s in such a way that we can easily recognize a pattern.

P = 14+ 5

or

$P = 14+ 5 \times 1$

For the second triangle, the perimeter is ,

P =7 + 7 + 5 + 5

$P = 14+ 5 \times 2$

For the third rectangle the perimeter is

P = 7 + 7 + 5 + 5 + 5

$P = 14+ 5 \times 3$

For the nth triangle the perimeter is,

$P = 7 + 7+ 5 + 5 + 5 + ...n \: times$

$P = 14+ 5 \times n$

This implies,

P = 14+ 5n

Method 2: Using the formula

We can write the perimeter as the sequence,

19,24,29,...

where the first term is
a = 19

and the constant difference is
d = 24 - 19 = 29 - 24 = 5

The nth term is given by the formula,

P(n) = a + (n - 1)d

This simplifies to,

P(n) = 5n + 14

The correct answer is B.

ANSWER TO QUESTION 2

We examine the y-coordinates of the relation to see if there is a constant difference.

46 - 39 = 39 - 32 = 32 - 25 = 7

Since there is a constant difference, it means the relationship is linear.

To determine whether it is decreasing or increasing, we need to find the slope using any two points.

$Slope = \frac{46 - 39}{0 - 1} = - \frac{7}{1} = - 7$

Since the slope is negative, the relationship is a function that is decreasing.

Therefore the function is decreasing and linear.

The correct answer is C.

ANSWER TO QUESTION 3

For the ordered pair
( 1, 3 )

$x = 1 \: and \: y = 3$

The relation between x and y is that,

$y = {3}^{1} = 3$

For the ordered pair,

( 2, 9 ),

$x = 2 \: and \: y = 9$

Their relation between x and y is,

$y = {3}^{2} = 9$

For the ordered pair
( 3, 27 )

$x = 3 \: \: and \: \: y = 27$

The relation is
$y = {3}^{3} = 27$
Also,

( 4, 81 )

$y = {3}^{4} = 81$

and finally,

( 5, 243 )

$y = {3}^{5} = 243$
In each case we raise 3 to the exponent of the x-value to get the y-value.

So in general, if we have
(x,y)

the rule will be
$y = {3}^{x}$

The correct answer is C.

ANSWER TO QUESTION 4

For the ordered pair,

( 1, 36 ),

$x = 1 \: \: and \: y = 36$
This implies that,

$y = {6}^{2}$
we can rewrite in terms of the x-value to obtain,

$y = (1 + 5) ^{2}$

For the ordered pair,

( 2, 49 ),

$x = 2 \: \: and \: \: y = 49$
This implies that,
$y = {7}^{2}$

We can rewrite this in terms of x-value to get,

$y = {(2 + 5)}^{2}$
Similarly

$y = 64 \Rightarrow \: y = {(3 + 5)}^{2}$

$y = 81 \Rightarrow \: y = {(4 + 5)}^{2}$
$y = 100 \Rightarrow \: y = {(5 + 5)}^{2}$

Therefore the rule is
$y = {(x+ 5)}^{2}$

The correct answer is C.

Mathematics

Will get brainiest and points 1. write an equation that relates the number of triangles in the figure (n), to the perimeter of the figure (p) a. the equation for the perimeter is p = 5n + 7 b. the equation for the perimeter is p = 5n + 14 c. the equation for the perimeter is p = 7n + 10 d. the equation for the perimeter is p = 7n + 5 2. the table shows the relationship between the number of sports teams a person belongs to and the amount of free time the person has each week. number of sports teams | free time (hours) 0 46 1 39 2 32 3 25 is the

Step-by-step answer

P Answered by PhD

ANSWER TO QUESTION 1

Method 1: Observing a pattern.

Perimeter is the distance around the triangle.

For the first triangle, the perimeter is

P = 7 + 7 + 5

Let us write the sum of the 7s and 5s in such a way that we can easily recognize a pattern.

P = 14+ 5

or

$P = 14+ 5 \times 1$

For the second triangle, the perimeter is ,

P =7 + 7 + 5 + 5

$P = 14+ 5 \times 2$

For the third rectangle the perimeter is

P = 7 + 7 + 5 + 5 + 5

$P = 14+ 5 \times 3$

For the nth triangle the perimeter is,

$P = 7 + 7+ 5 + 5 + 5 + ...n \: times$

$P = 14+ 5 \times n$

This implies,

P = 14+ 5n

Method 2: Using the formula

We can write the perimeter as the sequence,

19,24,29,...

where the first term is
a = 19

and the constant difference is
d = 24 - 19 = 29 - 24 = 5

The nth term is given by the formula,

P(n) = a + (n - 1)d

This simplifies to,

P(n) = 5n + 14

The correct answer is B.

ANSWER TO QUESTION 2

We examine the y-coordinates of the relation to see if there is a constant difference.

46 - 39 = 39 - 32 = 32 - 25 = 7

Since there is a constant difference, it means the relationship is linear.

To determine whether it is decreasing or increasing, we need to find the slope using any two points.

$Slope = \frac{46 - 39}{0 - 1} = - \frac{7}{1} = - 7$

Since the slope is negative, the relationship is a function that is decreasing.

Therefore the function is decreasing and linear.

The correct answer is C.

ANSWER TO QUESTION 3

For the ordered pair
( 1, 3 )

$x = 1 \: and \: y = 3$

The relation between x and y is that,

$y = {3}^{1} = 3$

For the ordered pair,

( 2, 9 ),

$x = 2 \: and \: y = 9$

Their relation between x and y is,

$y = {3}^{2} = 9$

For the ordered pair
( 3, 27 )

$x = 3 \: \: and \: \: y = 27$

The relation is
$y = {3}^{3} = 27$
Also,

( 4, 81 )

$y = {3}^{4} = 81$

and finally,

( 5, 243 )

$y = {3}^{5} = 243$
In each case we raise 3 to the exponent of the x-value to get the y-value.

So in general, if we have
(x,y)

the rule will be
$y = {3}^{x}$

The correct answer is C.

ANSWER TO QUESTION 4

For the ordered pair,

( 1, 36 ),

$x = 1 \: \: and \: y = 36$
This implies that,

$y = {6}^{2}$
we can rewrite in terms of the x-value to obtain,

$y = (1 + 5) ^{2}$

For the ordered pair,

( 2, 49 ),

$x = 2 \: \: and \: \: y = 49$
This implies that,
$y = {7}^{2}$

We can rewrite this in terms of x-value to get,

$y = {(2 + 5)}^{2}$
Similarly

$y = 64 \Rightarrow \: y = {(3 + 5)}^{2}$

$y = 81 \Rightarrow \: y = {(4 + 5)}^{2}$
$y = 100 \Rightarrow \: y = {(5 + 5)}^{2}$

Therefore the rule is
$y = {(x+ 5)}^{2}$

The correct answer is C.

StudenGPT

Name: Geometry Date: Per: Unit 4: Congruent Triangles Quiz 4-1: Classifying and Solving for Sides/Angles in Triangles Directions: If is the midpoint of , Classify each triangle by its angles and sides. 1. : 2. : 3. : 4. : 5. If , and classify by its sides. Show all work to justify your answer. Classify: Find all missing angles. 6. 7. Solve for . 8. 9. 0 Gina Wilson (All Things Algebra), 2014

Step-by-step answer

P Answered by Studen AI

1

To solve this quiz, we will go through each question step by step.

1. Triangle CFE:
Since GF is the midpoint of AB, we have FG = GA and FG = GB. So, CF and EF are congruent. Since FE = EF, triangle CFE is an isosceles triangle.

2. Triangle BEC:
Similarly, since GF is the midpoint of AB, we have GF = GA and GF = GB. So, BE and CE are congruent. Thus, triangle BEC is an isosceles triangle.

3. Triangle BFG:
GF is the midpoint of AB, so GF = GA and GF = GB. Therefore, BF and FG are congruent. In addition, since GF is the midpoint of AB, FG is also congruent to AG and GB. Hence, triangle BFG is an equilateral triangle.

4. Triangle GAF:
GF is the midpoint of AB, so GF = GA and GF = GB. Therefore, GF is congruent to AF. Similarly, since GF is the midpoint of AB, FG is congruent to AG and GB. Hence, triangle GAF is an isosceles triangle.

5. Triangle WXY:
To find the lengths of WX, XY, and WY, we can use the distance formula:
Distance = √((x2-x1)^2 + (y2-y1)^2)

WX = √((-3 - (-10))^2 + (-1 - 4)^2)
= √(7^2 + (-5)^2)
= √(49 + 25)
= √74

XY = √((-5 - (-3))^2 + (11 - (-1))^2)
= √((-2)^2 + (12)^2)
= √(4 + 144)
= √148

WY = √((-5 - (-10))^2 + (11 - 4)^2)
= √((-5)^2 + 7^2)
= √(25 + 49)
= √74

Therefore, WX ≈ 8.6, XY ≈ 12.2, and WY ≈ 8.6. Triangle WXY is an isosceles triangle because WX = WY.

6. Missing angles:
Unfortunately, the angles are not provided in the given information. We cannot provide specific values for these angles without additional information.

7. Missing angles:
Similarly, the angles for which we need to find the measures are not specified. Without the details, we cannot determine the values of these angles.

8. Solve for x:
The problem does not provide any equation or expression for x. Without any mathematical information, we cannot solve for x.

9. Solve for x:
Similar to the previous question, there is no equation or expression given to solve for x. Therefore, we cannot find the value of x.

StudenGPT

Name: Draloc Date: Per: Geometry Unit 4: Congruent Triangles Quiz 4-1: Classifvina and Solving for Sides/Angles in Triangles Directions: If is the midpoint of , classify each triangle by its angles and sides. 1. : 2. : 3. : 4. : Distance Formula 5. If , and classify by its sides. Show all work to justify your answer. Classify: Find all missing angles. 6. 7. Solve for . 8. 9.

Step-by-step answer

P Answered by Studen AI

1

Sure, let's go through the steps to solve this geometry task. 1. $\triangle C F E$ : Since $G$ is the midpoint of $\overline{AB}$, we can use the midpoint theorem to conclude that $\overline{CG}$ and $\overline{FG}$ are equal in length. Therefore, $\triangle CFE$ is an isosceles triangle. 2. $\triangle B E C$ : Since $G$ is the midpoint of $\overline{AB}$, we can use the midpoint theorem to conclude that $\overline{BG}$ and $\overline{CG}$ are equal in length. Therefore, $\triangle BEC$ is an isosceles triangle. 3. $\triangle B F G$ : Since $G$ is the midpoint of $\overline{AB}$, we can use the midpoint theorem to conclude that $\overline{BG}$ and $\overline{FG}$ are equal in length. Therefore, $\triangle BFG$ is an isosceles triangle. 4. $\triangle G A F$ : Since $G$ is the midpoint of $\overline{AB}$, we can use the midpoint theorem to conclude that $\overline{GA}$ and $\overline{GF}$ are equal in length. Therefore, $\triangle GAF$ is an isosceles triangle. 5. Classifying $\triangle WXY$ by its sides: To classify $\triangle WXY$ by its sides, we can use the distance formula to calculate the lengths of each side. \[ \begin{align*} WX &= \sqrt{(-3 - (-10))^2 + (-1 - 4)^2} \\ &= \sqrt{49 + 25} \\ &= \sqrt{74} \\ \\ XY &= \sqrt{(-5 - (-3))^2 + (11 - (-1))^2} \\ &= \sqrt{4^2 + 12^2} \\ &= \sqrt{16 + 144} \\ &= \sqrt{160} \\ \\ WY &= \sqrt{(-5 - (-10))^2 + (11 - 4)^2} \\ &= \sqrt{5^2 + 7^2} \\ &= \sqrt{25 + 49} \\ &= \sqrt{74} \end{align*} \] By comparing the lengths of the sides, we can see that $WX$ and $WY$ are equal, while $XY$ is different. Therefore, $\triangle WXY$ is an isosceles triangle. 6. Finding missing angles: We need additional information to find the missing angles. Please provide the angles or any other relevant data related to this question. 7. Finding missing angles: Similar to question 6, we need more information about the angles before we can provide the missing angle measurements. 8. Solving for $x$: To solve for $x$, we would need an equation or more information related to this question. Please provide the equation or any additional data required for solving this. 9. Similar to question 8, we would need specific equations or additional information to solve for $x$. Please provide the necessary details related to this question. If you can provide the missing information or clarify the equations, I'll be glad to assist you further in solving the remaining questions.

Mathematics

10 What are the x- and y-coordinates of point E, which partitions the directed line segment from A to B into a ratio of 1:2? B(-4,9) 9 8 X E ( mn)(x2 – xı) + x 7- 6 5 4 mm. )(x2 - y) + y 3 -7 -6 -5 4 -3 -2 -14 2 3 4 5 6 7 0 (0, 1) 0 (-1,3) O(-2,5) (1,0) X -2. 3 A(2,-3) 19

Step-by-step answer

P Answered by Specialist

Step-by-step explanation:

The formulas to find the x and y coordinates of E are:

$x=\frac{bx_1+ax_2}{a+b}$ and $y=\frac{by_1+ay_2}{a+b}$ where x1, x2, y1, and y2 are from the coordinates of A and B, and a = 1 (from the ratio) and b = 2 (from the ratio). Filling in to find x first:

$x=\frac{2(2)+1(-4)}{1+2}=\frac{4-4}{3}=0$ and now for y:

$y=\frac{2(-3)+1(9)}{1+2}=\frac{-6+9}{3}=\frac{3}{3}=1$

The coordinates of E are (0, 1).

Mathematics

10 What are the x- and y-coordinates of point E, which partitions the directed line segment from A to B into a ratio of 1:2? B(-4,9) 9 8 X E ( mn)(x2 – xı) + x 7- 6 5 4 mm. )(x2 - y) + y 3 -7 -6 -5 4 -3 -2 -14 2 3 4 5 6 7 0 (0, 1) 0 (-1,3) O(-2,5) (1,0) X -2. 3 A(2,-3) 19

Step-by-step answer

P Answered by Specialist

Step-by-step explanation:

The formulas to find the x and y coordinates of E are:

$x=\frac{bx_1+ax_2}{a+b}$ and $y=\frac{by_1+ay_2}{a+b}$ where x1, x2, y1, and y2 are from the coordinates of A and B, and a = 1 (from the ratio) and b = 2 (from the ratio). Filling in to find x first:

$x=\frac{2(2)+1(-4)}{1+2}=\frac{4-4}{3}=0$ and now for y:

$y=\frac{2(-3)+1(9)}{1+2}=\frac{-6+9}{3}=\frac{3}{3}=1$

The coordinates of E are (0, 1).

Mathematics

1. tony and his sister maria have the same birthday but tony is five years older than maria. let the variable x represent tony s age and y represent maria s age. which graph represents the relationship between tony s age and maria s age? 2. solve the equation: 3 ( x -7 ) - x = 2x - 21 a) 7 b) -2 c) infinitely many solutions d) no solution 3. which equation is an identity? a. 8-(5x+2)=-5x-6 b. 7z+10-z=8z-2(z-5) c. 8m-4=5m+8-m d. 6y+5=6y-5 4. which equation has no solution? a) 7v+2=8v-3 b) 3x-5=3x+8-x c) 4y+5=4y-6 d) 7z+6=-7z-5

Step-by-step answer

P Answered by PhD

21

Question 1:

Let Maria's age be 'x'
and Tony's age be 'x+5'

Turning this expression into a linear equation, we have
y = x + 5

Any linear equation will have the same form, y = mx + c, where m is the gradient and c is the y-intercept.

Matching this to y = x + 5, we have the gradient = 1 and the y-intercept = 5

The graph that shows a positive gradient and crosses the y-axis at 5 is the first graph (attached again below)

------------------------------------------------------------------------------------------------------------

Question 2:

Given the equation:
3(x-7)-x=2x-21

⇒ expanding the bracket
3x-21-x=2x-21

⇒ collecting like terms
2x-21=2x=21

Notice that the expression on the Left Hand Side is exactly the same with the expression on the Right Hand Side, this means the value of 'x' can be any value

Option C
----------------------------------------------------------------------------------------------------------------

Question 3

An identity is when the Left Hand Side expression and the Right Hand Side is exactly the same. Let's check for each equation:

Option A:
8-(5x+2)=-5x-6

⇒ Multiplying out the bracket
8-5x-2=-5x-6

⇒ Not an identity

Option B:
7z+10-z=8z-2(z-5)

⇒ Identity

Option C:
8m-4=5m+8-m

⇒ Not identity

Option D:
6y+5=6y-5

⇒ Not identity

Option B
---------------------------------------------------------------------------------------------------------------

Question 4

Option A:
7v+2=8v-3

⇒ the equation have a solution

Option B:
3x-5=3x+8-x

⇒ The equation has one solution

Option C:
4y+5=4y-6

⇒ The equation has no solution

Option D:
7z+6=-7z-5

$z=- \frac{11}{14}$ ⇒ The equation has one solution

Option C

1. tony and his sister maria have the same birthday but tony is five years older than maria. let the

Mathematics

1. tony and his sister maria have the same birthday but tony is five years older than maria. let the variable x represent tony s age and y represent maria s age. which graph represents the relationship between tony s age and maria s age? 2. solve the equation: 3 ( x -7 ) - x = 2x - 21 a) 7 b) -2 c) infinitely many solutions d) no solution 3. which equation is an identity? a. 8-(5x+2)=-5x-6 b. 7z+10-z=8z-2(z-5) c. 8m-4=5m+8-m d. 6y+5=6y-5 4. which equation has no solution? a) 7v+2=8v-3 b) 3x-5=3x+8-x c) 4y+5=4y-6 d) 7z+6=-7z-5

Step-by-step answer

P Answered by PhD

21

Question 1:

Let Maria's age be 'x'
and Tony's age be 'x+5'

Turning this expression into a linear equation, we have
y = x + 5

Any linear equation will have the same form, y = mx + c, where m is the gradient and c is the y-intercept.

Matching this to y = x + 5, we have the gradient = 1 and the y-intercept = 5

The graph that shows a positive gradient and crosses the y-axis at 5 is the first graph (attached again below)

------------------------------------------------------------------------------------------------------------

Question 2:

Given the equation:
3(x-7)-x=2x-21

⇒ expanding the bracket
3x-21-x=2x-21

⇒ collecting like terms
2x-21=2x=21

Notice that the expression on the Left Hand Side is exactly the same with the expression on the Right Hand Side, this means the value of 'x' can be any value

Option C
----------------------------------------------------------------------------------------------------------------

Question 3

An identity is when the Left Hand Side expression and the Right Hand Side is exactly the same. Let's check for each equation:

Option A:
8-(5x+2)=-5x-6

⇒ Multiplying out the bracket
8-5x-2=-5x-6

⇒ Not an identity

Option B:
7z+10-z=8z-2(z-5)

⇒ Identity

Option C:
8m-4=5m+8-m

⇒ Not identity

Option D:
6y+5=6y-5

⇒ Not identity

Option B
---------------------------------------------------------------------------------------------------------------

Question 4

Option A:
7v+2=8v-3

⇒ the equation have a solution

Option B:
3x-5=3x+8-x

⇒ The equation has one solution

Option C:
4y+5=4y-6

⇒ The equation has no solution

Option D:
7z+6=-7z-5

$z=- \frac{11}{14}$ ⇒ The equation has one solution

Option C

1. tony and his sister maria have the same birthday but tony is five years older than maria. let the

Mathematics

1. scientists estimate the rate of the wildebeest running at full speed to be 66 feet per second. write a function rule to describe the relationship between the time, t, and the distance ,d, a wildebeest travels when running at full speed.(1 point) a. t = 66d b. 66 = d • t c. d = 66/t d. d = 66t 2. identify the function rule shown in the table. (1 point) n 3 4 5 6 y 2 1 0 -1 a. y = 2 + n b. y = 5n c. y = 5 - n d. not enough information 3. rico made a function table to illustrate the rate he charges for mowing lawns. complete the table. then write

Step-by-step answer

P Answered by PhD

8

1. d. d = 66t

The maximum speed of the wildebeest is v=66 ft/s. Speed is defined as the ratio between the distance covered (d) and the time taken (t):

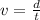
$v=\frac{d}{t}$

Re-arranging the formula, we get

d=vt

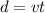
And substituting v=66 ft/s, we find

d=66t

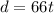
2. c. y = 5 - n

In fact, we can check that this rule satisfies all the numbers of the sequence:

n=3 --> y = 5 - 3 = 2

n=4 --> y = 5 - 4 = 1

n=5 --> y = 5 - 5 = 0

n=6 --> y = 5 - 6 = -1

3. d. $5.50, $11.00, $16.50; E = 5.50h

In fact, if we use the rule E=5.50 h, we see that the table is completed as follows:

h=1 --> E=(5.50)(1 h)=5.50$

h=2 --> E=(5.50)(2 h)=11.00 $

h=3 --> E=(5.50)(3 h)=16.50$

h=4 --> E=(5.50)(4 h)=22.00$

h=5 --> E=(5.50)(5 h)=27.50$

4. c. if d ≥ 5 then C = 4.70d, if d < 5 then C = 4.70d - 1; $17.80, $32.90

If the number of days is more than 5, the cost is 4.70$ per day, therefore c=4.70d (where d is the number of days); if the number of days is less than 5, one dollar is returned, so the cost will be C=4.70d-1. By applying this rule, we can calculate the rental cost after d=4 days and d=7 days:

- d=4 --> c=4.70*4-1=17.80$

- d=7 --> c=4.70*7=32.90$

5. b. y = 3x + 3

In fact, we can check this is the correct rule by substituting the numbers:

x=0 --> y=3*0+3=3

x=1 --> y=3*1+3=6

x=2 --> y=3*2+3=9

x=3 --> y=3*3+3=12

x=4 --> y=3*4+3=15

7. x -2 -1 0 1 2

y (-16 ) (-6 ) (4 ) (14 ) (24 )

The rule we have to apply is:

-10x + y = 4

Re-arranging it, we can solve for y:

y = 10x + 4

So, let's substitute the different values of x:

x=-2 --> 10*(-2)+4=-20+4= -16

x=-1 --> 10*(-1)+4=-10+4= -6

x=0 --> 10*0+4= 4

x=1 --> 10*1+4=10+4= 14

x=2 --> 10*2 +4 =20+4 = 24

8. y = -5x - 1

In fact, if substitute the different values of x given by the problem, we find:

x = -2 --> y = -5*(-2) -1= 10 -1 = 9

x = -1 --> y = -5*(-1) -1 = 5 -1 = 4

x = 0 --> y = -5*0 -1 = -1

x = 1 --> y = -5*1 - 1 = -6

x = 2 --> y = -5*2 -1 = -11

Given that a = ( − 6 7 ) and b = ( − 1 − 3 ) . If a − b = ( x y ) , work out the values of x and y .

Step-by-step answer

Faq

Try asking the Studen AI a question.