1. The correct option is D.
2. The correct option is C.
3. The correct option is D.
4. The correct option is B.
5. The correct option is D.
Step-by-step explanation:
The slope intercept form of a line is
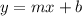
where, m is slope and b is y-intercept.
The slope of parallel lines are same.
(1)
The required line is parallel to the line y=-x-2 and passes through (2,-2). Slope of the line is -1.
The equation of required line is
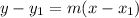
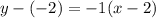
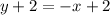
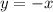
Therefore the correct option is D.
(2)
The required line is parallel to the line y=-3/2x+6 and passes through (2,-1). Slope of the line is -3/2.
The equation of required line is
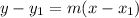
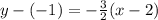
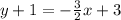
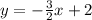
Therefore the correct option is C.
(3)
The required line is parallel to the line x=-3 and passes through (4,2). Slope of the line is infinite.
The equation of required line is
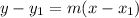
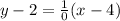
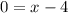
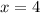
Therefore the correct option is D.
(4)
Product of slopes of perpendicular lines is -1.
The required line is perpendicular to the line y=1/2x-1 and passes through (-2,3). Slope of the required line is -2.
The equation of required line is
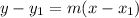
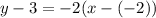
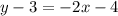
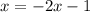
Therefore the correct option is B.
(5)
The required line is perpendicular to the line y+1=2(x-3) and passes through (5,0). Slope of the required line is -1/2.
The equation of required line is
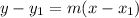
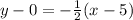
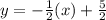
Therefore the correct option is D.