Use a calculator to find the value of each expression, №18009785, 28.12.2021 19:21

Mathematics

Use a calculator to find the value of each expression rounded to two decimal places. Make sure you are in Radian Mode. cos-(0.75)

Step-by-step answer

P Answered by Master

If you meant to write $\cos^{-1}(0.75)$ , then using a calculator in radian mode would show $\cos^{-1}(0.75) \approx 0.722734$

Rounding to the nearest hundredth gets us $\cos^{-1}(0.75) \approx 0.72$

Mathematics

The value, V (t), in dollars, of a stock t months after it is purchased is modeled by the following equation. V(t)= 42(1-e ^-1.5t) +36 a) V (1) =$. (Round to two decimal places as needed) V (12) =$.(Round to two decimal places as needed) b)Find V (t)=.(Simply your answer. Use intergers or decimal for any numbers in the expression. Round to one decimal place as needed) c) After how many months will the value of the stock first reach $75?( Do not round until the final answer. Then round to one decimal place as needed) d)lim V (t)= $ t-- [infinity]

Step-by-step answer

P Answered by Specialist

Step-by-step explanation: $V(t)= 42(1-e ^{1.5t} ) +36$ is given value in dollars of a stock in t months after it is purchased.

a) Substitute 1 for t

$V(1) = 42(1-e^{-1.5} )+36 \\=67.852\\=67.85$

V(12) = $V(1) = 42(1-e^{-1.5*12} )+36 \\=77.00$

b) Find derivative for V

$V'(t) = 42(-1.5) e^{-1.5t} )\\\\=-63e^{-1.5t}$

c) When V(t) = 75

$V(t)=75= 42(1-e ^{1.5t} ) +36\\1-e ^{1.5t=0.9286\\=-2.639$

d) As t tends to infinity, exponent being in negative t tends to 0

So V tends to 42(1-0)+36 = 78

Mathematics

The value, V (t), in dollars, of a stock t months after it is purchased is modeled by the following equation. V(t)= 42(1-e ^-1.5t) +36 a) V (1) =$. (Round to two decimal places as needed) V (12) =$.(Round to two decimal places as needed) b)Find V (t)=.(Simply your answer. Use intergers or decimal for any numbers in the expression. Round to one decimal place as needed) c) After how many months will the value of the stock first reach $75?( Do not round until the final answer. Then round to one decimal place as needed) d)lim V (t)= $ t-- [infinity]

Step-by-step answer

P Answered by Master

Step-by-step explanation: $V(t)= 42(1-e ^{1.5t} ) +36$ is given value in dollars of a stock in t months after it is purchased.

a) Substitute 1 for t

$V(1) = 42(1-e^{-1.5} )+36 \\=67.852\\=67.85$

V(12) = $V(1) = 42(1-e^{-1.5*12} )+36 \\=77.00$

b) Find derivative for V

$V'(t) = 42(-1.5) e^{-1.5t} )\\\\=-63e^{-1.5t}$

c) When V(t) = 75

$V(t)=75= 42(1-e ^{1.5t} ) +36\\1-e ^{1.5t=0.9286\\=-2.639$

d) As t tends to infinity, exponent being in negative t tends to 0

So V tends to 42(1-0)+36 = 78

Mathematics

A biologist observed a population of bacteria that grew at a rate expressed by the exponential equation f(t) = 256e0.06111) where t is in minutes. How long will it take the population to reach 5 times its initial value? Round to two decimal places and do not include t = in your answer.

Step-by-step answer

P Answered by PhD

It will take 26.34 minutes for the population to reach 5 times its initial value

Step-by-step explanation:

Exponential Growing

The population of bacteria grows at a rate expressed by the equation:

$f(t)=256e^{0.06111t}$

Where t is in minutes.

We need to know when the population will reach 5 times its initial value. The initial value can be determined by setting t=0:

$f(0)=256e^{0.06111\cdot 0}=256\cdot 1=256$

Now we find the time when the population is 5*256=1,280. The equation to solve is:

$1,280=256e^{0.06111t}$

Dividing by 256:

$e^{0.06111t}=1,280/256=5$

Taking natural logarithms:

$ln\left(e^{0.06111t}\right)=ln5$

Applying the logarithm properties:

0.06111t=ln5

Solving for t:

t=ln5/0.06111=26.34

It will take 26.34 minutes for the population to reach 5 times its initial value

Mathematics

A biologist observed a population of bacteria that grew at a rate expressed by the exponential equation f(t) = 256e0.06111) where t is in minutes. How long will it take the population to reach 5 times its initial value? Round to two decimal places and do not include t = in your answer.

Step-by-step answer

P Answered by PhD

It will take 26.34 minutes for the population to reach 5 times its initial value

Step-by-step explanation:

Exponential Growing

The population of bacteria grows at a rate expressed by the equation:

$f(t)=256e^{0.06111t}$

Where t is in minutes.

We need to know when the population will reach 5 times its initial value. The initial value can be determined by setting t=0:

$f(0)=256e^{0.06111\cdot 0}=256\cdot 1=256$

Now we find the time when the population is 5*256=1,280. The equation to solve is:

$1,280=256e^{0.06111t}$

Dividing by 256:

$e^{0.06111t}=1,280/256=5$

Taking natural logarithms:

$ln\left(e^{0.06111t}\right)=ln5$

Applying the logarithm properties:

0.06111t=ln5

Solving for t:

t=ln5/0.06111=26.34

It will take 26.34 minutes for the population to reach 5 times its initial value

Mathematics

The count in a culture of bacteria was 600 after 2 hours and 38,400 after 6 hours. (a) What is the relative rate of growth of the bacteria population? Express your answer as a percentage. (Round your answer to the nearest whole number.) % (b) What was the initial size of the culture? (Round your answer to the nearest whole number.) bacteria (c) Find a function that models the number of bacteria n(t) after t hours. (Enter your answer in the form n0ert. Round your n0 value to the nearest whole number. Round your r value to two decimal places.) n(t)

Step-by-step answer

P Answered by PhD

The bacteria has an exponential growth rate and the population of the

bacteria increases rapidly with time.

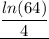
(a) The relative rate of growth is $\underline{\dfrac{ln(64)}{4}}$ .

(b) The initial size of the culture is 75 bacteria.

(c) The function that models the number of bacteria n(t) is; $\underline{n(t) = 75 \cdot e^{1.04 \cdot t}}$

(d) The number of bacteria after 4.5 hours is approximately 8,100 bacteria.

(e) The number of hours after which the bacteria will reach 75,000 is approximately 6.64 hours.

Reasons:

The count in the culture of bacteria after 2 hours = 600

The count after 6 hours = 38,400

(a) The relative rate of growth, k is given by the formula;

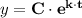
$y = \mathbf{C \cdot e^{k \cdot t}}$

Therefore, we get;

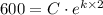
$600 = C \cdot e^{k \times 2}$

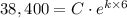
$38,400= C \cdot e^{k \times 6}$

Which gives;

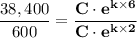
$\dfrac{38,400}{600} = \mathbf{\dfrac{C \cdot e^{k \times 6}}{C \cdot e^{k \times 2}}}$

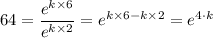
$64= \dfrac{e^{k \times 6}}{e^{k \times 2}} = e^{k \times 6- k \times 2} = e^{4\cdot k}$

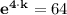
$\mathbf{e^{4\cdot k}} = 64$

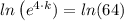
$ln\left(e^{4\cdot k}) = ln(64)$

4·k = ㏑(64)

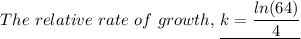
$The \ relative \ rate \ of \ growth, \, \underline{ k = \dfrac{ln(64)}{4}}$

(b) The initial size of the culture, C, is given by the relation;

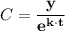
$C = \mathbf{\dfrac{y}{e^{k \cdot t}}}$

Therefore, we get;

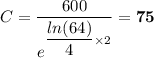
$C = \dfrac{600}{e^{\dfrac{ln(64)}{4} \times 2}} = \mathbf{ 75}$

The initial size of the culture, C = 75

(c) The function is 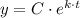$y = C \cdot e^{k \cdot t}$

Where:

y = n(t)

C = n₀

k = r

We get;

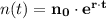
$n(t) = \mathbf{n_0 \cdot e^{r \cdot t}}$

n₀ = C = 75

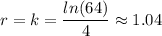
$r = k = \dfrac{ln(64)}{4} \approx 1.04$

Which gives the function as follows; $\underline{n(t) = 75 \cdot e^{1.04 \cdot t}}$

(d) The number of bacteria after 4.5 hours is 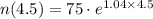$n(4.5) = 75 \cdot e^{1.04 \times 4.5}$ ≈ 8,100 bacteria

(e) At n(t) = 75,000, we have;

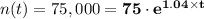
$n(t) = 75,000 = \mathbf{75 \cdot e^{1.04 \times t}}$

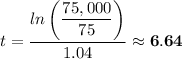
$t = \dfrac{ln\left(\dfrac{75,000}{75} \right)}{1.04} \approx \mathbf{6.64}$

The time at which the bacteria population will reach 75,000, t ≈ 6.64 hours.

Learn more here:

link

Mathematics

Imran is paid ?286 per week Every week he puts 20% of his wage into a savings account How much does he put into his savings each week

Step-by-step answer

P Answered by PhD

The answer is in the image

Mathematics

Neil places £2000 in a bank account that pays 1.5% simple interest per year. How much interest will he earn in 6 years?

Step-by-step answer

P Answered by PhD

SI=(P*R*T)/100

P=2000

R=1.5

T=6

SI=(2000*1.5*6)/100

=(2000*9)/100

=180

Neil will earn interest of 180

Mathematics

An ice cream shop offers 5 different flavors of ice cream and 9 different toppings. How many choices are possible for a single serving of ice cream with one topping?

Step-by-step answer

P Answered by PhD

For 1 flavor there are 9 topping

Therefore, for 5 different flavors there will be 5*9 choices

No of choices= 5*9

=45

Mathematics

Deanna gets 3 problems incorrect on a math quiz. Her score is 85%. How many questions are on the quiz?

Step-by-step answer

P Answered by PhD

The answer is in the image

Use a calculator to find the value of each expression rounded to two decimal places. Make sure you are in Radian Mode. cos-(0.75)

Step-by-step answer

Faq

Try asking the Studen AI a question.