Question 1
Given
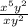
Substituting x = 0 and y = 0 gives
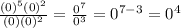
Let's check option A
We have
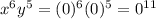
Let's check option B
We have
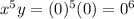
Let's check option C
We have
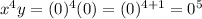
Let's check option D
We have
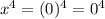
The expression that gives the same power with
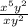
is the option D
Option D
------------------------------------------------------------------------------------------------------------
Question 2
We will check each option to see which one doesn't give the final value 125
Option A
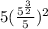
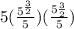
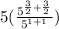
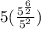
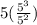
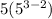
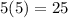
Option B
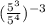
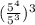
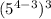
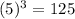
Option C
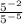
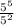
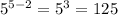
Option D
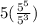
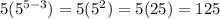
Option A
---------------------------------------------------------------------------------------------------------------
Question 3
Setting out the sum we have
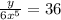
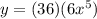
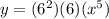
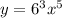
Option B
------------------------------------------------------------------------------------------------------------
Question 4
Given
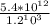
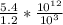
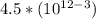

Option B
-------------------------------------------------------------------------------------------------------------
Question 5
Option A is CORRECT - when you divide two powers with the same base, you'd subtract the power ⇒ 5³ ÷ 5² = 5³⁻² = 5¹
Option B is INCORRECT - When two powers with the same base are subtracted from each other, we'd have to work out the value of each base first before subtracting, i.e. 6³ - 6² = 216 - 36 = 180 ⇒ This isn't the same by doing
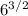
which would give an answer of 14.7
Option C is CORRECT - Multiplying two powers with the same base is by adding the power, i.e. 4³ × 4² = 4³⁺² = 4⁵
Option D is CORRECT - Raising a power by a power is the same as multiplying the two powers, i.e. (12²)³ = 12⁽²⁾⁽³⁾ = 12⁶
ANSWER: Option B