Prove that 1/sin^2A -1/tan^2A= 1

Step-by-step explanation:

Hint: 1 - Cos² A = Sin² A

To prove that:

LHS =

Using basic trigonometric identity,

Using trigonometric identity:

      = 1

      = RHS

LHS = RHS

Hence proved.

To prove that:

LHS =

Using basic trigonometric identity,

Using trigonometric identity:

      = 1

      = RHS

LHS = RHS

Hence proved.

1.

The annual net cost savings promised by the automated welding machine

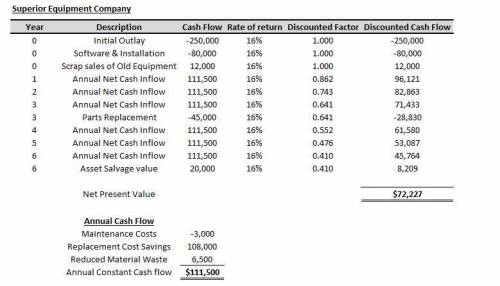
Annual Costs savings in replacing 6 welders $108,000

Reduced Material costs $6,500

Total annual Costs savings = $114,500

Note there is a $3,000 annual maintenance cost that will then be taken off this savings amount to make up the Annual Net cash inflow of $111,500

2

A. The Net Present value is $72,227. Kindly refer to the attached document for the clear presentation

B. The project should be accepted because it delivers a positive NPV. Meaning the net benefit outweighs the cost of owning the new Assets.

3.

The Discounted net Cash flow for the 6 years (aside the initial outlay) is $402,227.

Annually this comes to $67,038.

The benefit the business gets in the switch to the automatic welders is approximately $67,038 annually.

The total nom of  code that can be used is equal to 5+3 = 8

The answer is in the image 

The answer is in the image 

The solution is given in the image below

The wood before starting =12 feet

Left wood=6 feet

Wood used till now=12-6=6 feet

Picture frame built till now= 6/(3/4)

=8 pieces

Therefore, till now 8 pieces have been made.