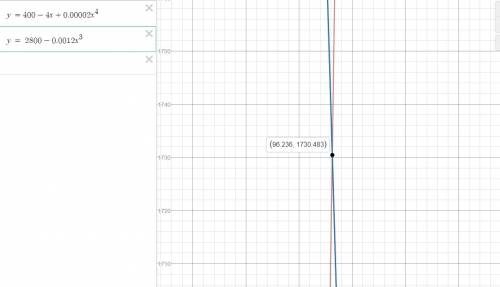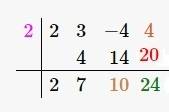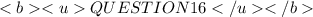
If the demand and supply are equal, then we equate the two functions in p and solve for p.
That is
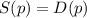
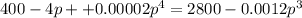
We can rearrange to obtain,
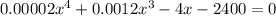
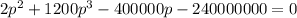
The real roots of this polynomial equation are:
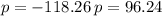
Since price can not be negative, we discard the negative value ,
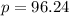
The correct answer for question 16 is C.
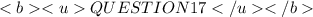
We were given the solution to this polynomial as
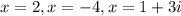
We need to recognize the presence of the complex root and treat it nicely.
There is one property about complex roots of polynomial equations called the complex conjugate property. According to this property, if
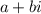
is a solution to
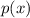
then the complex conjugate

is also a root.
Since
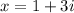
is a solution then,
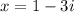
is also a solution.
Therefore we have
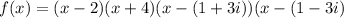
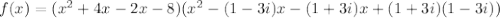
We expand to obtain,
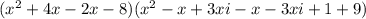
Note that:
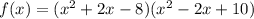
We now expand to obtain,
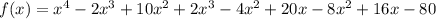
We simplify further to obtain,
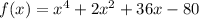
The correct answer for question 17 is A.
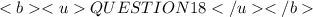
If
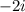
is a zero of the polynomial,
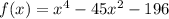
then the complex conjugate
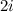
is also a zero,
This means that ,
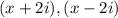
are factors of the polynomial.
The product of these two factors,
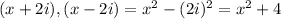
is also a factor , so we use it to divide and get the remaining factors.
see diagram for long division.
The above polynomial can therefore factored completely as,
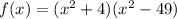
Applying our knowledge from difference of two squares, we obtain,

Hence all the zeroes of these polynomial can be found by setting
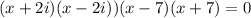
This implies,
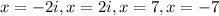
The correct answer for question 18 is B
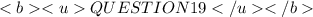
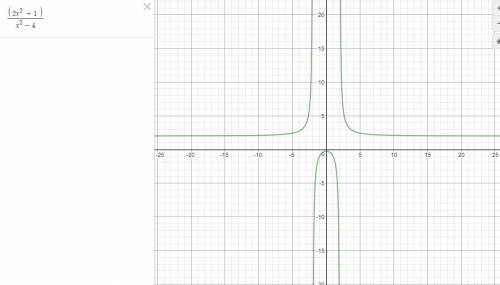
We were asked to find the horizontal and vertical asymptote of
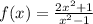
To find the horizontal asymptote, divide the term with the highest degree in the numerator by the term with the highest degree in the denominators. That is the horizontal asymptote is given by,
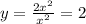
For vertical asymptote, equate the denominator to zero and solve for x.
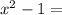
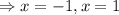
None of the options is correct, so the correct answer for question 19 is A.
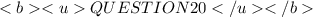
We are converting,
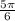
to degrees .
To convert from radians to degrees, multiply by,
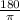
That is,
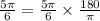
We simplify to obtain,
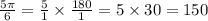
The correct answer is B.
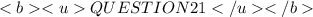
Recall the mnemonics, SOH CAH TOA
The sine ratio is given by,
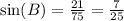
From the diagram,
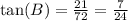
The correct answer is C.
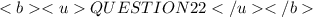
From the above diagram, We can determine the value of x using the sine or cosine ratio, depending on where the 17 is placed.
Using the cosine ratio, we obtain,
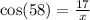
We can simply switch positions to make x the subject.
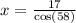
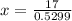
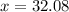
Hence the correct answer is A.
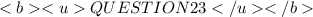
Coterminal angles have the same terminal sides.
To find coterminal angles, we keep adding or subtracting 360 degrees.
See diagram.
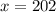
is coterminal with
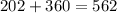
or
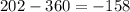
The correct answer is D.
See the attached file for continuation.