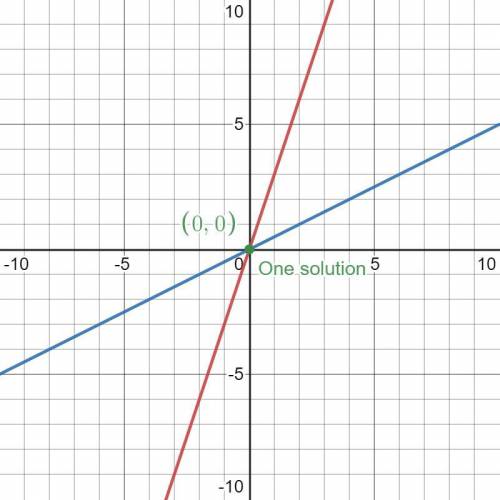
1. Independent
2. (4, -1)
3. (4, 3)
4. (2,5)
5. (2, -1)
6. (10, -1)
7. (2, -3)
8. (1/3, 2/3)
9. 4 and 3
10. (4,-1)
Step-by-step explanation:
1.If a system has one or more solution then it is called Consistent system.
If a system has no solution then it is called an Inconsistent system.
If Consistent system has exactly one solution then it is called Dependent
and If the Consistent system has an infinite number of the solution then it is called Independent.
Therefore, If a system has exactly one solution it is called Dependent.
2. The equations we have:
y = -x + 3 and y = -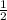 +3
+3
After solving these equations, We get, x = 4, y = -1
3. The substitution method is we substitute the value of x or y from one equation to another equation and solve them.
After solving given equations. We get,
x = 4, y = 3
4. Similarly, We solve both equations, we get
x = 2, y = 5
5. In the Elimination method, firstly we equate either coefficient of x or y in both equations (if either coefficient of x or y is not equal) after that we add or subtract both equations to eliminate one variable and solve them.
After solving given equations. We get,
x = 2, y = -1
9. We get equations,
x+y=7 and 4(7-y) = 5y+1
After solving these we get the value of x and y.
10. The point of intersection is the solution of both equations. Here we see the point of intersection is (4, -1)