Mathematics : asked on rosie20052019

21.04.2022

Integral of x/(x + 1)²(x+2)²

Step-by-step answer

09.07.2023, solved by verified expert

Rajat Thapa

s Specialist

Mathematics, DAV Post Graduate College

3 137

5 229 answers

4.9 rating

Unlock the full answer

I suppose you mean the integral

Break up the integrand into partial fractions:

Solve for the coefficients:

So we have

It is was helpful?

Helpful Useless

Faq

Mathematics

Integral of x/(x + 1)²(x+2)²

Step-by-step answer

P Answered by Specialist

I suppose you mean the integral

$\displaystyle \int \frac{x}{(x+1)^2 (x+2)^2} \, dx$

Break up the integrand into partial fractions:

$\dfrac{x}{(x+1)^2 (x+2)^2} = \dfrac{a}{x+1} + \dfrac{b}{(x+1)^2} + \dfrac{c}{x+2} + \dfrac{d}{(x+2)^2}$

$\dfrac{x}{(x+1)^2 (x+2)^2} \\ = \dfrac{a(x+1)(x+2)^2 + b(x+2)^2 + c(x+1)^2(x+2) + d(x+1)^2}{(x+1)^2 (x+2)^2}$

$\dfrac{x}{(x+1)^2 (x+2)^2} \\ = \dfrac{(a+c)x^3+(5a+b+4c+d)x^2+(8a+4b+5c+2d)x + 4a+4b+2c+d}{(x+1)^2(x+2)^2}$

x = (a+c)x^3+(5a+b+4c+d)x^2+(8a+4b+5c+2d)x + 4a+4b+2c+d

Solve for the coefficients:

$\begin{cases}a+c=0 \\ 5a+b+4c+d=0 \\ 8a+4b+5c+2d=1 \\ 4a+4b+2c+d=0\end{cases} \implies a=3,b=-1,c=-3,d=-2$

So we have

$\displaystyle \int \frac{x}{(x+1)^2 (x+2)^2} \, dx= \int \left(\frac3{x+1} - \frac1{(x+1)^2} - \frac3{x+2} - \frac2{(x+2)^2}\right) \, dx$

$\displaystyle \int \frac{x}{(x+1)^2 (x+2)^2} \, dx= 3\ln|x+1| + \frac1{x+1} - 3\ln|x+2| + \frac2{x+2} + C$

$\displaystyle \int \frac{x}{(x+1)^2 (x+2)^2} \, dx= \ln|x+1|^3 - \ln|x+2|^3 + \frac{3x+4}{(x+1)(x+2)} + C$

$\displaystyle \int \frac{x}{(x+1)^2 (x+2)^2} \, dx= \boxed{\ln\left|\frac{x+1}{x+2}\right|^3 + \frac{3x+4}{(x+1)(x+2)} + C}$

Mathematics

With cal 2 exercise involving integrals? i have to find the arc length of y = lnx given that 1 ≤ x ≤ sqrt (3) here is my procedure: i found the derivative of y = lnx and got, y = 1 / (x) 1 + (1/(x))^2 = 1 + (1/(x^2)) = (x^2+1)/(x^2) integral from 1 to sqrt 3 of sqrt((x^2+1/(x^2)) dx = sqrt ( x ^ 2 + 1 ) / ( x ) dx x = tan b dx = (sec^2)bdb sqrt(x^2+1) = sqrt ( (tan^2)b + 1) = sqrt ( (sec^2)b) = secb integral = ((sec)/(tanb)) times (sec^2)bdb and here comes the part i don t understand, in my exercise it becomes integral = ((sec^2)b)/((tan^2)b))

Step-by-step answer

P Answered by PhD

$\displaystyle\int\frac{\sqrt{x^2+1}}x\,\mathrm dx=\int\frac{\sqrt{\tan^2B+1}}{\tan B}\sec^2B\,\mathrm dB$

$\tan^2B+1=\sec^2B$

$\sqrt{\sec^2B}=\sec B$ (provided that $\sec B0$ )

Then

$\dfrac{\sec B}{\tan B}\cdot\sec^2B=\dfrac{\sec^2B}{\tan B}\cdot\sec B$

(just moving around a factor of $\sec B$ )

$\dfrac{\sec B}{\tan B}\cdot\sec^2B=\dfrac{\sec^2B}{\tan^2B}\cdot\sec B\tan B$

(multiply by $\dfrac{\tan B}{\tan B}$ )

Mathematics

Determine whether each integral is convergent or divergent. 1- 1/(x-2)^3/2 dx, limits ( infinite to 3) 2- (1/3-4x)dx, limits (0 to -infinite) 3- e^(-5p) dx, limits ( infinite to 2) 4- (x^2/(sqrt(1+x^3)))dx , limits ( infinite to 0) 5- lnx/x dx , limits(infinite to 1) 6- 1/(x^2 +x)dx , limits (infinite to 1) 7- 3/x^5 dx ,limits (1 to 0) 8- dx/(x+2)^1/4 , limits (14 to -2) 9- 1/(x-1)^1/3 , limits (9 to 0) 10- e^x /((e^x) -1), limits (1 to -1) 11- z^2 lnz dz ,limits( 2 to 0) 12- s={(x,y) | x = 1,0 = y =e^-x}

Step-by-step answer

P Answered by PhD

Divergers

Step-by-step explanation:

Mathematics

Step-by-step answer

P Answered by PhD

$\displaystyle\int\frac{\sqrt{x^2+1}}x\,\mathrm dx=\int\frac{\sqrt{\tan^2B+1}}{\tan B}\sec^2B\,\mathrm dB$

$\tan^2B+1=\sec^2B$

$\sqrt{\sec^2B}=\sec B$ (provided that $\sec B0$ )

Then

$\dfrac{\sec B}{\tan B}\cdot\sec^2B=\dfrac{\sec^2B}{\tan B}\cdot\sec B$

(just moving around a factor of $\sec B$ )

$\dfrac{\sec B}{\tan B}\cdot\sec^2B=\dfrac{\sec^2B}{\tan^2B}\cdot\sec B\tan B$

(multiply by $\dfrac{\tan B}{\tan B}$ )

Mathematics

Consider the following initial-value problem. (x + y)2 dx + (2xy + x2 − 2) dy = 0, y(1) = 1 Let ∂f ∂x = (x + y)2 = x2 + 2xy + y2. Integrate each term of this partial derivative with respect to x, letting h(y) be an

Step-by-step answer

P Answered by PhD

$(x+y)^2\,\mathrm dx+(2xy+x^2-2)\,\mathrm dy=0$

Suppose the ODE has a solution of the form F(x,y)=C , with total differential

$\dfrac{\partial F}{\partial x}\,\mathrm dx+\dfrac{\partial F}{\partial y}\,\mathrm dy=0$

This ODE is exact if the mixed partial derivatives are equal, i.e.

$\dfrac{\partial^2F}{\partial y\partial x}=\dfrac{\partial^2F}{\partial x\partial y}$

We have

$\dfrac{\partial F}{\partial x}=(x+y)^2\implies\dfrac{\partial^2F}{\partial y\partial x}=2(x+y)$

$\dfrac{\partial F}{\partial y}=2xy+x^2-2\implies\dfrac{\partial^2F}{\partial x\partial y}=2y+2x=2(x+y)$

so the ODE is indeed exact.

Integrating both sides of

$\dfrac{\partial F}{\partial x}=(x+y)^2$

with respect to gives

$F(x,y)=\dfrac{(x+y)^3}3+g(y)$

Differentiating both sides with respect to gives

$\dfrac{\partial F}{\partial y}=2xy+x^2-2=(x+y)^2+\dfrac{\mathrm dg}{\mathrm dy}$

$\implies x^2+2xy-2=x^2+2xy+y^2+\dfrac{\mathrm dg}{\mathrm dy}$

$\implies\dfrac{\mathrm dg}{\mathrm dy}=-y^2-2$

$\implies g(y)=-\dfrac{y^3}3-2y+C$

$\implies F(x,y)=\dfrac{(x+y)^3}3-\dfrac{y^3}3-2y+C$

so the general solution to the ODE is

$F(x,y)=\dfrac{(x+y)^3}3-\dfrac{y^3}3-2y=C$

Given that y(1)=1 , we find

$\dfrac{(1+1)^3}3-\dfrac{1^3}3-2=C\implies C=\dfrac13$

so that the solution to the IVP is

$F(x,y)=\dfrac{(x+y)^3}3-\dfrac{y^3}3-2y=\dfrac13$

$\implies\boxed{(x+y)^3-y^3-6y=1}$

Mathematics

Step-by-step answer

P Answered by PhD

$(x+y)^2\,\mathrm dx+(2xy+x^2-2)\,\mathrm dy=0$

Suppose the ODE has a solution of the form F(x,y)=C , with total differential

$\dfrac{\partial F}{\partial x}\,\mathrm dx+\dfrac{\partial F}{\partial y}\,\mathrm dy=0$

This ODE is exact if the mixed partial derivatives are equal, i.e.

$\dfrac{\partial^2F}{\partial y\partial x}=\dfrac{\partial^2F}{\partial x\partial y}$

We have

$\dfrac{\partial F}{\partial x}=(x+y)^2\implies\dfrac{\partial^2F}{\partial y\partial x}=2(x+y)$

$\dfrac{\partial F}{\partial y}=2xy+x^2-2\implies\dfrac{\partial^2F}{\partial x\partial y}=2y+2x=2(x+y)$

so the ODE is indeed exact.

Integrating both sides of

$\dfrac{\partial F}{\partial x}=(x+y)^2$

with respect to gives

$F(x,y)=\dfrac{(x+y)^3}3+g(y)$

Differentiating both sides with respect to gives

$\dfrac{\partial F}{\partial y}=2xy+x^2-2=(x+y)^2+\dfrac{\mathrm dg}{\mathrm dy}$

$\implies x^2+2xy-2=x^2+2xy+y^2+\dfrac{\mathrm dg}{\mathrm dy}$

$\implies\dfrac{\mathrm dg}{\mathrm dy}=-y^2-2$

$\implies g(y)=-\dfrac{y^3}3-2y+C$

$\implies F(x,y)=\dfrac{(x+y)^3}3-\dfrac{y^3}3-2y+C$

so the general solution to the ODE is

$F(x,y)=\dfrac{(x+y)^3}3-\dfrac{y^3}3-2y=C$

Given that y(1)=1 , we find

$\dfrac{(1+1)^3}3-\dfrac{1^3}3-2=C\implies C=\dfrac13$

so that the solution to the IVP is

$F(x,y)=\dfrac{(x+y)^3}3-\dfrac{y^3}3-2y=\dfrac13$

$\implies\boxed{(x+y)^3-y^3-6y=1}$

Mathematics

If f(x)=integral of sqrt(t^3+1) dt from 0 to x, then f (2)=?

Step-by-step answer

P Answered by Specialist

F'(2) = 3

$\int\limits^x_0 {\sqrt{t^3+1}} \, dt$

Using Fundamental Theorem of Calculus:

Since x = 2, you now have:

$\int\limits^2_0 {\sqrt{t^3+1} } \, dt$

so F'(x) = $\sqrt{t^3+1}$

--> F'(2) = $\sqrt{2^3+1}$ = $\sqrt{9}$ = 3

so F'(2) = 3

Mathematics

If f(x)=integral of sqrt(t^3+1) dt from 0 to x, then f (2)=?

Step-by-step answer

P Answered by Specialist

F'(2) = 3

$\int\limits^x_0 {\sqrt{t^3+1}} \, dt$

Using Fundamental Theorem of Calculus:

Since x = 2, you now have:

$\int\limits^2_0 {\sqrt{t^3+1} } \, dt$

so F'(x) = $\sqrt{t^3+1}$

--> F'(2) = $\sqrt{2^3+1}$ = $\sqrt{9}$ = 3

so F'(2) = 3

Mathematics

Example 3 (a) set up the integral for the length of the arc of the hyperbola xy = 3 from the point (1, 3) to the point 6, 1 2 . (b) use simpson s rule with n = 10 to estimate the arc length. solution (a) we have y = 3 x dy dx = and so the arc length is l = 6 1 + dy dx 2 dx 1 = 6 1 + 9 x4 dx 1 = 6 x4 + 9 x2 dx 1 . (b) using simpson s rule with a = 1, b = 6, n = 10, δx = 0.5, and f(x) = , we have l = 6 1 + 9 x4 dx 1 ≈ δx 3 [f(1) + 4f(1.5) + 2f(2) + 4f(2.5) + ⋯ + 2f(5) + 4f(5.5) + f(6)] ≈ (rounded to four decimal places).

Step-by-step answer

P Answered by Master

Step-by-step explanation:

Given is the function

xy =3

Use product rule to find derivative

xy'+y =0 OR 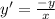$y'=\frac{-y}{x}$

Arc length = 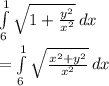$\int\limits^1_6 {\sqrt{1+\frac{y^2}{x^2} } } \, dx \\=\int\limits^1_6 {\sqrt{\frac{x^2+y^2}{x^2} } } \, dx \\\\$

Substitute y = 3/x

WE get

arc length = 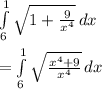$\int\limits^1_6 {\sqrt{1+\frac{9}{x^4} } } \, dx \\\\=\int\limits^1_6 {\sqrt{\frac{x^4+9}{x^4} } } \, dx \\$

Using simpson rule for 1/3 we have

x(x^4+9)^1/2f(x)2 times or 4 times

13.162277663.162277663.16227766

1.53.751.6666666676.666666667

251.25

2.56.9327123121.109233974.43693588

39.4868329811.054092553

3.512.611998261.0295508784.118203512

416.27882061.0174262872.034852575

4.520.47101611.0109143754.0436575

525.179356621.0071742652.01434853

5.530.398396341.0049056644.019622656

636.124783741.0034662152.00693243

6.542.356374961.0025177514.010071002

749.091750831.0018724662.003744932

7.556.329943191.0014212124.005684849

864.070273921.001098032.00219606

8.572.312256911.0008616874.00344675

981.055536521.0006856362.001371272

9.590.299847731.0005523294.002209318

10100.04498991.0004498992.000899798

10.5110.29080881.0003701484.00148059

11121.03718441.0003073092.000614618

11.5132.28402211.0002572564.001029023

12144.03124661.000216994.82148E-05

52.270413638.711735605

Answer is 8.7117

Mathematics

Let f(x,y)= (y^2+1i + (2xy-2)j. compute single integral with subscript of c f * dr where a). c is the straight path from (0,0) to (0,1) b,) c is the path from (0,0) to (0,1) along the parabola y=x^2

Step-by-step answer

P Answered by Specialist

I do not know if this is exactly what you are looking for

Let f(x,y)= (y^2+1i + (2xy-2)j. compute single integral with subscript of c f * dr where a). c is th

free Ask question

Today we have helped

986 students

just now

Biology

remained short for several centuries, then became much taller over the last 50 years. have consistently grown taller over the last two centuries. vary in height primarily because of the degree of various stressors on each population. vary in height because of genetic differences between groups.

p Answered by PhD

just now

Mathematics

Y=4x−9 with (3,_) as ordered pairs

m Answered by Master

just now

Mathematics

DJ Jacqueline is making a playlist for an internet radio show; she is trying to decide what 6 songs to play and in what order they should be played. If she has her choices narrowed down to 7 hip-hop, 14 pop, and 22 blues songs, and she wants to play an equal number of hip-hop, pop, and blues songs, how many different playlists are possible

p Answered by PhD

1 minute ago

Mathematics

Write the ratio as a fraction in simplest form.
24 to 20

p Answered by PhD

1 minute ago

Mathematics

1. 100 kilometers at 20 km/h? 2. 180 kilometers at 45 km/h?

Nonsense will be reported!!
Plss help me on this

s Answered by Specialist

Get help with homework

Integral of x/(x + 1)²(x+2)²

Step-by-step answer

Faq

Try asking the Studen AI a question.