Explanation:
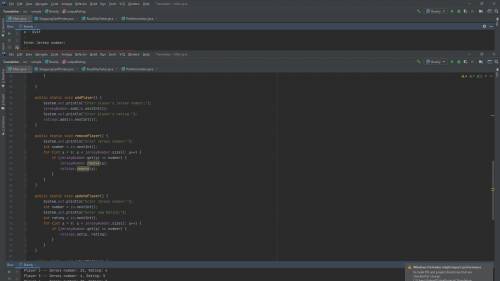
The following code is written in Java and loops five times asking for the desired inputs from the user and saves that information in two Vectors named jerseyNumber and ratings. Then creates a while loop for the menu and a seperate method for each of the options...
import java.util.Scanner;
import java.util.Vector;
class {
static Scanner in = new Scanner(System.in);
static Vector<Integer> jerseyNumber = new Vector<>();
static Vector<Integer> ratings = new Vector<>();
public static void main(String[] args) {
for (int x = 0; x < 5; x++) {
System.out.println("Enter player " + (x+1) + "'s jersey number:");
jerseyNumber.add(in.nextInt());
System.out.println("Enter player " + (x+1) + "'s rating:");
ratings.add(in.nextInt());
}
boolean reloop = true;
while (reloop == true) {
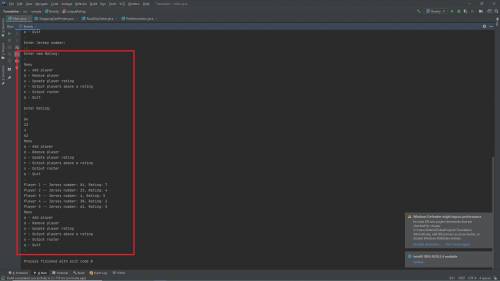
System.out.println("Menu");
System.out.println("a - Add player");
System.out.println("d - Remove player");
System.out.println("u - Update player rating");
System.out.println("r - Output players above a rating");
System.out.println("o - Output roster");
System.out.println("q - Quit");
char answer = in.next().charAt(0);
switch (answer) {
case 'a': addPlayer();
break;
case 'd': removePlayer();
break;
case 'u': updatePlayer();
break;
case 'r': outputRating();
break;
case 'o': outputRoster();
break;
case 'q': System.exit(0);
reloop = false;
break;
}
}
}
public static void addPlayer() {
System.out.println("Enter player's jersey number:");
jerseyNumber.add(in.nextInt());
System.out.println("Enter player's rating:");
ratings.add(in.nextInt());
}
public static void removePlayer() {
System.out.println("Enter Jersey number:");
int number = in.nextInt();
for (int x = 0; x < jerseyNumber.size(); x++) {
if (jerseyNumber.get(x) == number) {
jerseyNumber.remove(x);
ratings.remove(x);
}
}
}
public static void updatePlayer() {
System.out.println("Enter Jersey number:");
int number = in.nextInt();
System.out.println("Enter new Rating:");
int rating = in.nextInt();
for (int x = 0; x < jerseyNumber.size(); x++) {
if (jerseyNumber.get(x) == number) {
ratings.set(x, rating);
}
}
}
public static void outputRating() {
System.out.println("Enter Rating:");
int rating = in.nextInt();
for (int x = 0; x < ratings.size(); x++) {
if (ratings.get(x) >= rating) {
System.out.println(jerseyNumber.get(x));
}
}
}
public static void outputRoster() {
for (int x = 0; x < jerseyNumber.size(); x++) {
System.out.println("Player " + (x+1) + " -- Jersey number: " + jerseyNumber.get(x) + ", Rating: " + ratings.get(x));
}
}
}
0
13 785
rating
= 13
has a reference angle of 
.
.
,then 
, In QII, the secant ratio is negative.
is 
.
in the y-axis and shift it to the left by 
units, it coincides with graph of 
is a one-to-one function on the interval ![[-\frac{\pi}{2},\frac{\pi}{2}]](/tpl/images/0029/3850/8b799.png)
by the symmetric property of even functions.
on the interval;
This means that 
and 
This means 
or 
and 
.
.
.
![[2(\cos \frac{\pi}{9}+i\sin \frac{\pi}{9})]^3=2^3\cos 3\times \frac{\pi}{9}+i\sin 3\times \frac{\pi}{9})](/tpl/images/0029/3850/de0fb.png)
![[2(\cos \frac{\pi}{9}+i\sin \frac{\pi}{9})]^3=8(frac{2}{2})+i8(\frac{\sqrt{3}}{2})=4+4\sqrt{3}i](/tpl/images/0029/3850/dad44.png)
.
.
.
Get help with homework
