No, these equations are not parallel.
Step-by-step explanation:
The equation 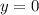 is a vertical line. This equation, in fact, is the y-axis.
is a vertical line. This equation, in fact, is the y-axis.
The equation 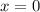 is a horizontal line. This equation, in fact, is the x-axis.
is a horizontal line. This equation, in fact, is the x-axis.
These lines are perpendicular, not parallel.