1. 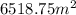
2. 295 m of fencing is needed
3. 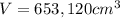
4. $18,480
5. Part 1: 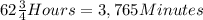
AND Part 2:
Mike Chewer 870 mins = 14.5 hours
Jennifer Glass 225 mins = 3.75 hours
Fred Carlton 75 mins = 1.25 hours
Amy Amaretto 720 mins = 12 hours
6. Part 1: $237.6; AND Part 2: 540 cm (or 5.4m)
7. Part 1: 6.3 m; AND Part 2: 96.8ºF
8. No.
9. Part 1: 15 kg = 33 pounds AND Part 2: 48.4 pounds = 22 kgs
10. 1.475 hours
Step-by-step explanation:
1. Area of car park is area of rectangle (length * width) - area of half circle of arena (half circle area is 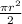
Length is given as 100 and width is 75, also the radius of the circle is half of 50, which is 25. Putting all of these we get:
Area of car park = 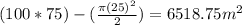
2. Looking at the diagram carefully, we can see that the perimeter (sum of all the sides) would be sum of top side (100 m), right side (75 m ), bottom side (100 m) and left side that is left ( area covers 50m and gate of 5 m, so covers 55m, left is 75 - 55 = 20)
Perimeter is 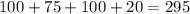 . So 295 m of fencing is needed
. So 295 m of fencing is needed
3. Volume of cylinder is 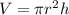
We need in cm, so we need to convert 1.3m to centimeters. Since there are 100 cm in 1 m, 1.3m is equal to 130 cm. Also, radius is half of 80cm, which is 40 cm. Putting these into the formula we get:
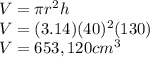
4. If $1.54 : £1 , then £12,000 would be 12,000 multiplied by 1.54. So:
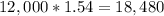 dollars
dollars
5. Part 1: To convert to minutes, we multiply 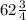 by 60. Thus we have
by 60. Thus we have 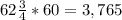 minutes
minutes
Part 2: Mike Chewer worked 870 minutes, to convert to hours, we divide by 60. So 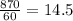 hrs
hrs
Jennifer Glass worked 225 minutes, to convert to hours, we divide by 60. So 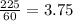 hrs
hrs
Fred Carlton worked 75 minutes, to convert to hours, we divide by 60. So 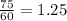 hrs
hrs
Amy Amaretto worked 720 minutes, to convert to hours, we divide by 60. So 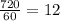 hrs
hrs
6. Part 1: If £1 = $1.76, to get australian dollars for £135, we multiply 135 by 1.76. So we have 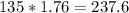
So that's $237.6
Part 2: Converting 8 m to cm, we multiply 8 by 100, so it is 8*100=800cm. Since both sides will be taken by 130 cm speakers, so a total space of 2*130=260cm will be taken. So amount of space left for the band, in cm, is 800 - 260 = 540 cm (or 5.4m)
7. Part 1: To convert cm to meters, we divide it by 100. So we have:
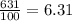
Rounding to 1 decimal place, it is 6.3m
Part 2: The formula to convert Celsius to Fahrenheight is 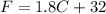
Plugging C=36 into this, we get F: 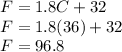 degrees
degrees
8. One item weights 0.76 kg so 40 items (in 1 box) would weigh 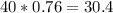 kg
kg
According to policy, it is over 30, so you won't be allowed to lift it. So, NO!
9. We can see that 1 kg is 2.2 lbs (conversion factor). So 15 kg is 15 * 2.2 = 33 pounds.
Also, To get pounds into kgs, we divide the pounds by 2.2. So 48.4 lbs is 48.4 divided by 2.2 which is 22 kg.
10. We need to divide 59 km by 40 to get the amount of time it will take (distance divided by rate is time). So 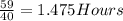
Second answer choice is a bit wrong, it should be 1.475 hours. Correct answer is 1.475 hours.