3. Consider the straight line x + y = 1 and the family of straight lines that pass through the origin given by y = mx. As m changes the line rotates about the
origin. Solve these two systems of linear equation and find their points of inter-
section. Is there always a solution - If yes, briefly explain why. If not - for what
a
values of m is there no solution.

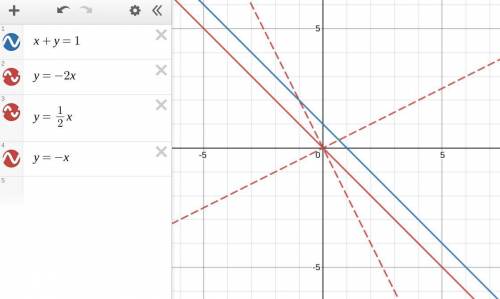
Step-by-step explanation:

Two distinct lines will always have a point of intersection, provided they are not parallel. That is, the system of equations {x +y = 1, y = mx} will have a unique solution as long as m ≠ -1.

The solution to the system can be found by substitution:

  x +mx = 1

  x(1 +m) = 1 . . . . factor out x

  x = 1/(1+m) . . . . . divide by the coefficient of x; we must have m ≠ -1

  y = m/(1+m) . . . . find the y-coordinate of the solution

The point of intersection is (1/(1+m), m/(1+m)).

__

The above solution is undefined when the denominator is zero: m = -1. There is no solution for m = -1.

The answer is in the image 

SI=(P*R*T)/100

P=2000

R=1.5

T=6

SI=(2000*1.5*6)/100

=(2000*9)/100

=180

Neil will earn interest of 180

Cost of 7 gallons=$24.50

Cost of 1 gallon=24.50/7=3.5

Cost of 15 gallons=15*3.5=52.5

Cost of 15 gallons will be $52.5

The answer is in the image 

Salesperson will make 6% of 1800

=(6/100)*1800

=108

Salesperson will make $108 in $1800 sales

Salesperson will make 6% of 1800

=(6/100)*1800

=108

Salesperson will make $108 in $1800 sales

tip=18% of 75.45

     =18/100 * 75.45 = $13.581

Tip = $13.581

Cost of 6 gallons =$15

Cost of 1 gallon =15/6

                           =$2.5

Cost of 7 gallons=$2.5 * 7

                           =$17.5

The answer is in the image