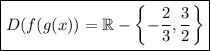ℝ - {(-2/3),(3/2)}
Step-by-step explanation:
We want the domain of f(g(x)). So, firstly, we have to find the domain for g(x) and, then, for f(g(x)).
- Domain of g(x): Since the expression is a fracion, we must exclude the values of x that make null the denominator. Hence,

- Domain of f(g(x)): We'll find its expression:
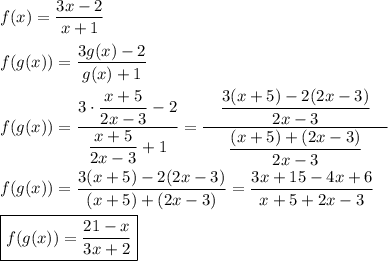
Now, once again, we have to exclude the values of x that make the denominator equals to zero. Thus,
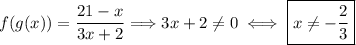
Lastly, we may write the domanin of f(g(x)):
![D(f(g(x)) = \left]-\infty,-\dfrac{2}{3}\right[\cup\left]-\dfrac{2}{3},\dfrac{3}{2}\right[\cup\left]\dfrac{3}{2},\infty\right[](/tpl/images/0889/7130/14df0.png)
or, just writing in a shorter way: