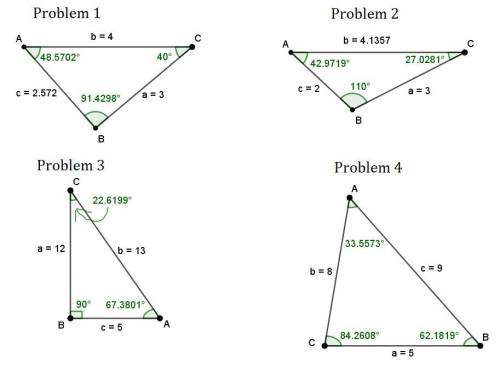
The missing values are highlighted in bold, which are approximate to four decimal places (with the exception of B = 90 in problem 3).
Lowercase letters a,b,c are side lengths; Uppercase letters A,B,C are angles opposite the sides mentioned.
The drawings are shown below.
==========================================================
Explanation:
Problem 1
Use the Law of Cosines to solve for side c
c^2 = a^2 + b^2 - 2*a*b*cos(C)
c^2 = 3^2 + 4^2 - 2*3*4*cos(40)
c^2 = 6.61493337
c = sqrt(6.61493337)
c = 2.57195128
c = 2.5720
Now apply the Law of Sines to find angle A
sin(A)/a = sin(C)/c
sin(A)/3 = sin(40)/2.57195128
sin(A) = 3*sin(40)/2.57195128
sin(A) = 0.74976647
A = arcsin(0.74976647)
A = 48.57015285
A = 48.5702
Once we know two angles of a triangle, we can then subtract their sum from 180 to get the third missing angle.
A+B+C = 180
B = 180 - (A+C)
B = 180 - (48.57015285+40)
B = 91.42984715
B = 91.4298
-----------------------------------
Problem 2
Like with the previous problem, we can use the Law of Cosines to solve for the missing side.
b^2 = a^2 + c^2 - 2*a*c*cos(B)
b^2 = 3^2 + 2^2 - 2*3*2*cos(110)
b^2 = 17.10424172
b = sqrt(17.10424172)
b = 4.13572747
b = 4.1357
Now use the Law of Sines to find angle A
sin(A)/a = sin(B)/b
sin(A)/3 = sin(110)/4.13572747
sin(A) = 3*sin(110)/4.13572747
sin(A) = 0.68164014
A = arcsin(0.68164014)
A = 42.9719427
A = 42.9719
Then we can wrap things up like so
A+B+C = 180
C = 180 - (A+B)
C = 180 - (42.9719427+110)
C = 27.0280573
C = 27.0281
-----------------------------------
Problem 3
Use the Law of Cosines to find angle A.
a^2 = b^2 + c^2 - 2*b*c*cos(A)
12^2 = 13^2 + 5^2 - 2*13*5*cos(A)
144 = 194 - 130*cos(A)
-130*cos(A) = 144 - 194
-130*cos(A) = -50
cos(A) = (-50)/(- 130)
cos(A) = 0.38461538
A = arccos(0.38461538)
A = 67.38013505
A = 67.3801
We could use the Law of Cosines to find angle B, but I'll use the Law of Sines instead.
sin(A)/a = sin(B)/b
sin(B) = b*sin(A)/a
sin(B) = 13*sin(67.38013505)/12
sin(B) = 0.99999999998574
sin(B) = 1
B = arcsin(1)
B = 90
It turns out we have a 5-12-13 right triangle (though usually c is the longest side instead of b).
Now we could use the Law of Cosines to find angle C, but the steps shown below are much quicker in my opinion that don't involve any trig functions.
A+B+C = 180
C = 180 - (A+B)
C = 180 - (67.38013505 + 90)
C = 22.61986495
C = 22.6199
-----------------------------------
Problem 4
The steps will basically be identical to problem 3, but with different numbers of course.
First we need the Law of Cosines to find angle A.
a^2 = b^2 + c^2 - 2*b*c*cos(A)
5^2 = 8^2 + 9^2 - 2*8*9*cos(A)
25 = 145 - 144*cos(A)
-144*cos(A) = 25 - 145
-144*cos(A) = -120
cos(A) = (-120)/(-144)
cos(A) = 0.83333333
A = arccos(0.83333333)
A = 33.55730976
A = 33.5573
Now use the Law of Sines to find angle B.
sin(A)/a = sin(B)/b
sin(B) = b*sin(A)/a
sin(B) = 8*sin(33.55730976)/5
sin(B) = 0.88443328
B = arcsin(0.88443328)
B = 62.18186103
B = 62.1819
Lastly,
A+B+C = 180
C = 180 - (A+B)
C = 180 - (33.55730976 + 62.18186103)
C = 84.26082921
C = 84.2608
-----------------------------------
Side notes:
The phrasing "solve the triangle" means to find all three sides and all three angles.Each answer is approximate with the exception of B = 90 in problem 3.Intermediate calculations were done to eight decimal places. The final answers are to four decimal places. In the first two problems, we can prove only one triangle is possible due to the SAS triangle congruence theorem.For the last two problems, only one triangle is possible because of the SSS triangle congruence theorem.I used GeoGebra to make each triangle shown below.