If 7 is mean of 10,3,4,a,6,9,10. Find the value of a

a = 7

Step-by-step explanation:

Given:

7 is mean of 10,3,4,a,6,9,10

To Find:

Value of a

Solve:

Mean →

⇒ 42+a=49

Subtract 42 from both sides

x + 42 - 42 = 49 - 42

Simplify

⇒ a=7  

~Learn with Lenvy~

I'm not really sure because I have not done this in a while but I think True

Step-by-step explanation:

...

I'm not really sure because I have not done this in a while but I think True

Step-by-step explanation:

...

Explained below.

Step-by-step explanation:

A two-sample test is to be performed to determine whether the mean weight loss for those on low-carbohydrate or Mediterranean diets is greater than the mean weight loss for those on a conventional low-fat diet.

(a)

The hypothesis can be defined as follows:

H₀: μ₁ - μ₂ ≤ 0 vs. Hₐ: μ₁ - μ₂ > 0

(b-1)

Use Excel to perform the t test for independent samples.

The output is attached below.

The test statistic value is, t = 7.58.

(b-2)

The degrees of freedom is, df = 58.

The critical value is, t₅₈ = 1.672.

The rejection region is:

Rejected H₀ if t > t₅₈ = 1.672.

(c)

Decision:

t = 7.58 > t₅₈ = 1.672

The null hypothesis will be rejected at 5% level of significance.

Thus, the nutritionist can conclude that overweight people on low-carbohydrate or Mediterranean diets lost more weight than people on a conventional low-fat diet.

The correct option is Yes.

Explained below.

Step-by-step explanation:

A two-sample test is to be performed to determine whether the mean weight loss for those on low-carbohydrate or Mediterranean diets is greater than the mean weight loss for those on a conventional low-fat diet.

(a)

The hypothesis can be defined as follows:

H₀: μ₁ - μ₂ ≤ 0 vs. Hₐ: μ₁ - μ₂ > 0

(b-1)

Use Excel to perform the t test for independent samples.

The output is attached below.

The test statistic value is, t = 7.58.

(b-2)

The degrees of freedom is, df = 58.

The critical value is, t₅₈ = 1.672.

The rejection region is:

Rejected H₀ if t > t₅₈ = 1.672.

(c)

Decision:

t = 7.58 > t₅₈ = 1.672

The null hypothesis will be rejected at 5% level of significance.

Thus, the nutritionist can conclude that overweight people on low-carbohydrate or Mediterranean diets lost more weight than people on a conventional low-fat diet.

The correct option is Yes.

.model small

.stack 100h

.data

prompt db 13, 10, 'First number:','$'

prompt db 13,10, 'Second number:', '$'

result db 13, 10, 'Sum','$'

Explanation:

See attach image

Step-by-step explanation:

a)

Here researcher claims that the mean weight loss for those on  low-carbohydrate or Mediterranean diets is greater than the mean  weight loss for those on a conventional low-fat diet

Set the null and alternative hypotheses to test the above claim as below.

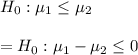versus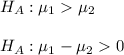

b)

Assume that the variance of the two populations are equal.

Under the null hypothesis, the test statistics is defined as

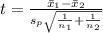
where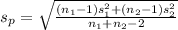

Use the foll owing Excel instructions and conduct the above test.

Step1: Enter the datainto two columns of spreadsheet.

Step2: Select Data Analysis from Data ribbon.

Step3: Select t-test. Two-sample Assuming equal variances.

Step4: Input the data range for variable 1 and variable 2.

Step5: Enter 0 as the Hypothesized Mean Difference.

Step6: Click OK.

Thus, the resultant outout is as follows:

                                                       Low-carb                        Low-fat

Mean                                               9.773333333       6.283333333

Variance                                          3.197885057                    3.160747126

Observations                                  30                                      30

Pooled Variance                             3.179316092

Hypothesized Mean Difference     0

df                                                      58

t Stat                                                 7.580610844

P(T < = t) one-tail                              1.54916E - 10

t Critical one — tail                           1.671552762

P(T <2) two-tail                                  3.09831E - 10

t Critical two - tail                              2.001717484

1) From the above output, the test statistics is obtained as t =  7.5806

2) From the above output, the critical value for one-tailed testis  obtained as

Rejection rule:  Reject 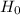if

c)

At 5% level of significance, the calculated value of test statistics  is greater than the critical value.

Therefore, reject the null hypothesis.

Hence, the nutritionist conclude that overweight people on  low-carbohydrate or Mediterranean diets lost more weight than  people on a conventional low-fat diet.