1. It is shifted 2 units down.
The graph of 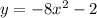 is shifted 2 units down with respect to the graph of
is shifted 2 units down with respect to the graph of 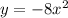 . We can prove this by taking, for instance, x=0, and calculating the value of y in the two cases. In the first function:
. We can prove this by taking, for instance, x=0, and calculating the value of y in the two cases. In the first function:
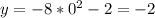
In the second function:
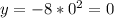
So, the first graph is shifted 2 units down.
2. 160.56 m
The path of the rocket is given by:
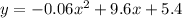
The problem asks us to find how far horizontally the rocket lands - this corresponds to find the value of x at which the height is zero: y=0. This means we have to solve the following equation
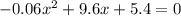
Using the formula,
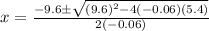
which has two solutions: 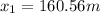 and
and 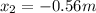 . The second solution is negative, so it has no physical meaning, therefore the correct answer is 160.56 m.
. The second solution is negative, so it has no physical meaning, therefore the correct answer is 160.56 m.
3. 27.43 m
The path of the rock is given by:
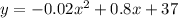
The problem asks us to find how far horizontally the rock lands - this corresponds to find the value of x at which the height is zero: y=0. This means we have to solve the following equation
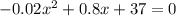
Using the formula,
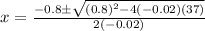
which has two solutions: 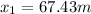 and
and 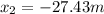 . In this case, we have to choose the second solution (27.43 m), since the rock was thrown backward from the initial height of 37 m, so the negative solution corresponds to the backward direction.
. In this case, we have to choose the second solution (27.43 m), since the rock was thrown backward from the initial height of 37 m, so the negative solution corresponds to the backward direction.
4. (-2, 16) and (1, -2)
The system is:
 (1)
(1)
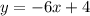 (2)
(2)
We can equalize the two equations:
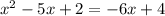
which becomes:
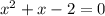
Solving it with the formula, we find two solutions: x=-2 and x=1. Substituting both into eq.(2):
x=-2 --> 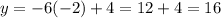
x=1 --> 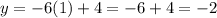
So, the solutions are (-2, 16) and (1, -2).
5. (-1, 1) and (7, 33)
The system is:
 (1)
(1)
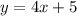 (2)
(2)
We can equalize the two equations:
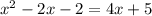
which becomes:
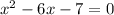
Solving it with the formula, we find two solutions: x=7 and x=-1. Substituting both into eq.(2):
x=7 --> 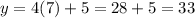
x=-1 --> 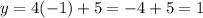
So, the solutions are (-1, 1) and (7, 33).
6. 2.30 seconds
The height of the object is given by:
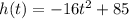
The time at which the object hits the ground is the time t at which the height becomes zero: h(t)=0, therefore
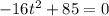
By solving it,
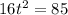
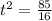
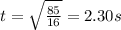
7. Reaches a maximum height of 19.25 feet after 0.88 seconds.
The height of the ball is given by
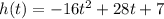
The vertical velocity of the ball is equal to the derivative of the height:
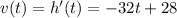
The maximum height is reached when the vertical velocity becomes zero: v=0, therefore when
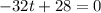
from which we find 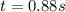
And by substituting these value into h(t), we find the maximum height:
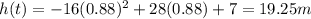
8. Reaches a maximum height of 372.25 feet after 4.63 seconds.
The height of the boulder is given by
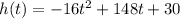
The vertical velocity of the boulder is equal to the derivative of the height:
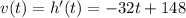
The maximum height is reached when the vertical velocity becomes zero: v=0, therefore when
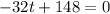
from which we find 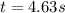
And by substituting these value into h(t), we find the maximum height:
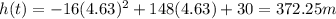
9. 12 m
Let's call x the length of the side of the original garden. The side of the new garden has length (x+3), so its area is
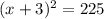
Solvign this equation, we find
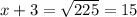
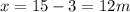
10. 225/4
In fact, if we write 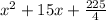 , we see this is equivalent to the perfect square:
, we see this is equivalent to the perfect square:
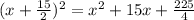
11. -11.56, 1.56
The equation is:
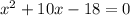
By using the formula:
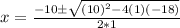
which has two solutions: x=-11.56 and 1.56.
12. -10.35, 1.35
The equation is:
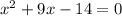
By using the formula:
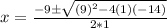
which has two solutions: x=-10.35 and 1.35.