1. Find m∠B, rounded to the nearest degree. a.53°, №18011170, 11.09.2021 13:42

Mathematics

1. Find m∠B, rounded to the nearest degree. a.53° b.35° c.44° d.65°

Step-by-step answer

P Answered by Master

53°

Step-by-step explanation:

Hypotenuse is the longest side and it is opposite to angle 90°

$\sf Sin \ B = \dfrac{Opposite \ side \ of \ angle \ B}{hypotenuse}\\\\$

$= \dfrac{4}{5}\\\\=0.8$

$B = Sin^{-1} \ (0.8)\\$

B = 53°

Mathematics

IS TIMED : Find tan–1 1.4281 to the nearest degree. a.10° c.5° b.55° d.35° Using a scientific calculator or graphing calculator find the inverse tangent of the ratio. Round to the nearest degree. 3/1 a.71° b.19° c.72° d.18° Using a scientific calculator or graphing calculator find the inverse tangent of the ratio. Round to the nearest degree. 1/1 a.45° b.90° c.0° d.1°

Step-by-step answer

P Answered by PhD

10

number 2 is 72 number 3 is 45 and number 1 makes no sense

Step-by-step explanation: hopes this helps god bess

Mathematics

IS TIMED : Find tan–1 1.4281 to the nearest degree. a.10° c.5° b.55° d.35° Using a scientific calculator or graphing calculator find the inverse tangent of the ratio. Round to the nearest degree. 3/1 a.71° b.19° c.72° d.18° Using a scientific calculator or graphing calculator find the inverse tangent of the ratio. Round to the nearest degree. 1/1 a.45° b.90° c.0° d.1°

Step-by-step answer

P Answered by PhD

10

number 2 is 72 number 3 is 45 and number 1 makes no sense

Step-by-step explanation: hopes this helps god bess

Mathematics

Need . i will give a and rate you 5 stars. 2. a tree that is 10 yards tall casts a shadow 14 yards long. find the angle of elevation from the tip of the shadow to the top of the tree. round to the nearest degree. a. 54 b. 36 c. 46 d. 44 3. use the law of sines to find the missing side of the triangle. find b. a. 70.1 b. 43.8 c. 57.1 d. 31.5 4. for a triangle abc, find the measure of ab given m a. 45.22 b. 96.68 c. 88.19 d. 81.12 5. use the law of cosines to solve the problem. on a baseball field, the pitchers mound is 60.5 feet from home plate.

Step-by-step answer

P Answered by Specialist

4

The angle of elevation will be given by:
tan θ=opposite/adjacent
tan θ=10/14
θ=arctan 10/14=
θ=35.5~26°

5. c^2=a^2+b^2-2abcos C
c^2=60.5²+216²-2*60.5*216cos34
c^2=28,648.524
c=169.255~169.3 ft

Mathematics

Need . i will give a and rate you 5 stars. 2. a tree that is 10 yards tall casts a shadow 14 yards long. find the angle of elevation from the tip of the shadow to the top of the tree. round to the nearest degree. a. 54 b. 36 c. 46 d. 44 3. use the law of sines to find the missing side of the triangle. find b. a. 70.1 b. 43.8 c. 57.1 d. 31.5 4. for a triangle abc, find the measure of ab given m a. 45.22 b. 96.68 c. 88.19 d. 81.12 5. use the law of cosines to solve the problem. on a baseball field, the pitchers mound is 60.5 feet from home plate.

Step-by-step answer

P Answered by Specialist

4

The angle of elevation will be given by:
tan θ=opposite/adjacent
tan θ=10/14
θ=arctan 10/14=
θ=35.5~26°

5. c^2=a^2+b^2-2abcos C
c^2=60.5²+216²-2*60.5*216cos34
c^2=28,648.524
c=169.255~169.3 ft

Mathematics

The formula to convert Fahrenheit to Celsius is C - 5 (F - 32). Convert 30°C to Fahrenheit. Round to the nearest degree. A. 30°F B. -1°F C. 112°F D. 86°F

Step-by-step answer

P Answered by PhD

8

D. *6F

Step-by-step explanation:

C=(F-32)*5/9

30=(F-32)*5/9

F = (30*9)/5+32

F = 86

Mathematics

+32. Convert 45°F to The formula to convert Celsius to Fahrenheit is F Celsius. Round to the nearest degree. O A. 49°C O B. 113°C O C. -1°C O D. 7°C

Step-by-step answer

P Answered by PhD

15

Option D. 7°C

Step-by-step explanation:

Let the temperature in Fahrenheit (F) and the temperature in Celsius(C)

The formula to convert Fahrenheit to Celsius is ⇒ F = 1.8 C + 32

So, to Convert 45° F to Celsius, substitute with with 45° F

45 = 1.8 C + 32

Solve for C

1.8 C = 45 - 32

1.8 C = 13

C = 13/1.8 = 7.222

Rounding to the nearest degree ⇒ 45° F = 7° C

The answer is option D. 7°C

Mathematics

The formula to convert Fahrenheit to Celsius is C - 5 (F - 32). Convert 30°C to Fahrenheit. Round to the nearest degree. A. 30°F B. -1°F C. 112°F D. 86°F

Step-by-step answer

P Answered by PhD

8

D. *6F

Step-by-step explanation:

C=(F-32)*5/9

30=(F-32)*5/9

F = (30*9)/5+32

F = 86

Mathematics

+32. Convert 45°F to The formula to convert Celsius to Fahrenheit is F Celsius. Round to the nearest degree. O A. 49°C O B. 113°C O C. -1°C O D. 7°C

Step-by-step answer

P Answered by PhD

15

Option D. 7°C

Step-by-step explanation:

Let the temperature in Fahrenheit (F) and the temperature in Celsius(C)

The formula to convert Fahrenheit to Celsius is ⇒ F = 1.8 C + 32

So, to Convert 45° F to Celsius, substitute with with 45° F

45 = 1.8 C + 32

Solve for C

1.8 C = 45 - 32

1.8 C = 13

C = 13/1.8 = 7.222

Rounding to the nearest degree ⇒ 45° F = 7° C

The answer is option D. 7°C

Mathematics

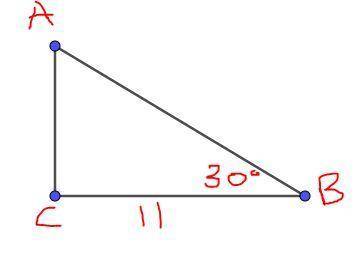
1. in abc, c is a right angle and bc= 11. if the measure of angle b= 30degrees, find ac. a) (11sqrt3)/3 b) 3sqrt/11 c)11/2 d)11sqrt3/2 2.which of the following angles has a reference angle of pi/8? a)-51pi/8 b)11pi/8 c)-33pi/8 d)27pi/8 3.your town’s public library is building a new wheelchair ramp to its entrance. by law, the maximum angle of incline for the ramp is 4.76 degrees. the ramp will have a vertical ride of 2.5 ft. what is the shortest horizontal distance that the ramp can span? a)11.9ft b)30.0ft c)4.3ft d)19.1ft 4. find the exact value

Step-by-step answer

P Answered by Specialist

1. The given triangle ABC, has a right angle at C, BC=11, and 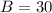$B=30\degree$

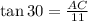
$\tan 30\degree=\frac{AC}{11}$

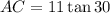
$AC=11\tan 30\degree$

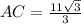
$AC=\frac{11\sqrt{3}}{3}$

Ans: A

2. The reference angle is the angle the terminal side makes with x-axis.

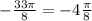
$-\frac{33\pi}{8}=-4\frac{\pi}{8}$

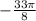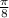This implies that, $-\frac{33\pi}{8}$ has a reference angle of $\frac{\pi}{8}$ .

Ans: C

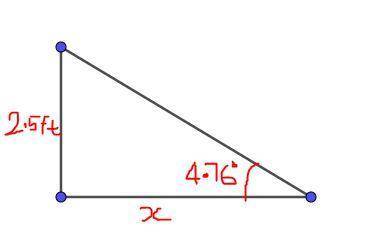
3. Let x be the shortest distance the ramp can span.

From the diagram; 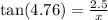$\tan (4.76\degree)=\frac{2.5}{x}$

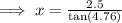
$\implies x=\frac{2.5}{\tan (4.76\degree)}$

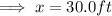
$\implies x=30.0ft$

Ans:B

4. Use the Pythagorean identity: 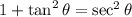$1+\tan ^2 \theta=\sec^2 \theta$ .

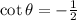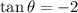
If $\cot \theta=-\frac{1}{2}$ ,then $\tan \theta=-2$

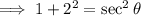
$\implies 1+2^2=\sec^2 \theta$

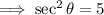
$\implies \sec^2 \theta=5$

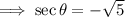$\implies \sec \theta=-\sqrt{5}$ , In QII, the secant ratio is negative.

Ans:C

5. We have 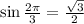$\sin \frac{2\pi}{3}=\frac{\sqrt{3} }{2}$

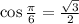
$\cos \frac{\pi}{6}=\frac{\sqrt{3} }{2}$

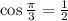
$\cos \frac{\pi}{3}=\frac{1}{2}$

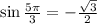
$\sin \frac{5\pi}{3}=-\frac{\sqrt{3} }{2}$

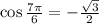
$\cos \frac{7\pi}{6}=-\frac{\sqrt{3} }{2}$

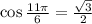
$\cos \frac{11\pi}{6}=\frac{\sqrt{3} }{2}$

Ans:A and D

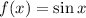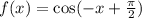6. The given function that is equivalent to $f(x)=\sin x$ is $f(x)=\cos (-x+\frac{\pi}{2})$ .

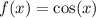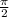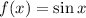When we reflect the graph of $f(x)=\cos (x)$ in the y-axis and shift it to the left by $\frac{\pi}{2}$ units, it coincides with graph of $f(x)=\sin x$ .

Ans:C

7. The function 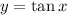$y=\tan x$ is a one-to-one function on the interval $[-\frac{\pi}{2},\frac{\pi}{2}]$

When we restrict the domain of 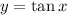$y=\tan x$ on $[-\frac{\pi}{2},\frac{\pi}{2}]$ it becomes an invertible function.

Ans: C

8. The given function is 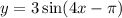$y=3\sin(4x-\pi)$

The horizontal shift is given by 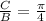$\frac{C}{B}=\frac{\pi}{4}$

The direction of the shift is to the right.

Ans:D

9. 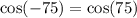$\cos(-75\degree)=\cos(75\degree)$ by the symmetric property of even functions.

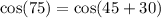
$\cos(75\degree)=\cos(45\degree+30\degree)$

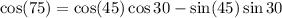
$\cos(75\degree)=\cos(45\degree) \cos30\degree-\sin(45\degree) \sin30\degree$

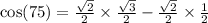
$\cos(75\degree)=\frac{\sqrt{2} }{2} \times \frac{\sqrt{3} }{2} -\frac{\sqrt{2} }{2} \times \frac{1}{2}$

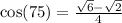
$\cos(75\degree)=\frac{\sqrt{6}-\sqrt{2}}{4}$

Ans: B

10. Recall the cosine rule: 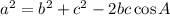$a^2=b^2+c^2-2bc\cos A$

Let the angle measure opposite to the longest side be A, then a=19,b=17, and c=15.

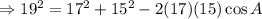
$\Rightarrow 19^2=17^2+15^2-2(17)(15)\cos A$

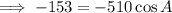
$\implies -153=-510\cos A$

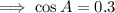
$\implies \cos A=0.3$

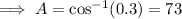
$\implies A=\cos^{-1}(0.3)=73\degree$

Ans:B

11. We want to solve 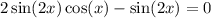$2\sin(2x)\cos(x)-\sin(2x)=0$ on the interval;

$[-\frac{\pi}{2},\frac{\pi}{2}]$

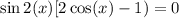
Factor: $\sin2(x)[2\cos(x)-1)=0$

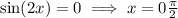
Either $\sin(2x)=0 \implies x=0\frac{\pi}{2}$

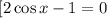Or $[2\cos x-1=0$ This means that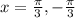 $x=\frac{\pi}{3},-\frac{\pi}{3}$

Therefore required solution is 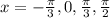$x=-\frac{\pi}{3},0,\frac{\pi}{3},\frac{\pi}{2}$

Ans:D

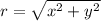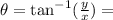
12. Use the relation: $r=\sqrt{x^2+y^2}$ and $\theta=\tan^{-1}(\frac{y}{x})=$

The given rectangular coordinate is (1,-2)

This implies that: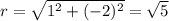 $r=\sqrt{1^2+(-2)^2}=\sqrt{5}$

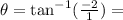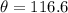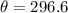
$\theta=\tan^{-1}(\frac{-2}{1})=$ This means $\theta=116.6$ or $\theta=296.6$

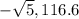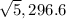
The polar forms are: $-\sqrt{5},116.6$ and $\sqrt{5},296.6$

Ans: B and C

13. The polar equation that represents an ellipse is

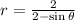$r=\frac{2}{2-\sin \theta}$ .

When written in standard form; 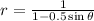$r=\frac{1}{1-0.5\sin \theta}$ .

The eccentricity is 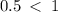$0.5\:$ .

Therefore the 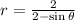$r=\frac{2}{2-\sin \theta}$ is an ellipse.

Ans: B

14. The DeMoivre’s Theorem states that;

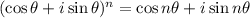
$(\cos \theta+i\sin \theta)^n=\cos n\theta+i\sin n\theta$

This implies that:

$[2(\cos \frac{\pi}{9}+i\sin \frac{\pi}{9})]^3=2^3\cos 3\times \frac{\pi}{9}+i\sin 3\times \frac{\pi}{9})$

$[2(\cos \frac{\pi}{9}+i\sin \frac{\pi}{9})]^3=8(frac{2}{2})+i8(\frac{\sqrt{3}}{2})=4+4\sqrt{3}i$

Ans: A

15. Let the initial point be (x,y), Then 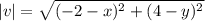$|v|=\sqrt{(-2-x)^2+(4-y)^2}$ .

If x=-8, and y=-4.

Then, 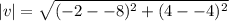$|v|=\sqrt{(-2--8)^2+(4--4)^2}$ .

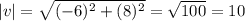$|v|=\sqrt{(-6)^2+(8)^2}=\sqrt{100}=10$ .

Ans: B

16. We find the dot product to see if it is zero.

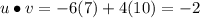
$u\bullet v=-6(7)+4(10)=-2$

Since the dot product is not zero the vectors are not orthogonal

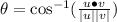
$\theta=\cos ^{-1}(\frac{u\bullet v}{|u||v|})$

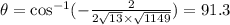
$\theta=\cos ^{-1}(-\frac{2}{2\sqrt{13}\times \sqrt{1149} }) =91.3\degree$

Ans:B

17. Given v=5i+4j, w=2i-3j.

u=v+w

Add corresponding components

This implies u=(5i+4j)+(2i-3j)

u=(5i+2i+4j-3j)

u=7i+j

Ans:B

See attachment.

1. in abc, c is a right angle and bc= 11. if the measure of angle b= 30degrees, find ac. a) (11sqrt3

1. Find m∠B, rounded to the nearest degree.

a.53°

b.35°

c.44°

d.65°

Step-by-step answer

Faq

Try asking the Studen AI a question.