Please help me with this #9

12

Step-by-step explanation:

Left:

Simplify the following:

-9 - -12

-(-12) = 12:

-9 + 12

-9 + 12 = 3:

3

Right:

Do the following addition:

-9 + 12

The number -9 is negative. Start from 0 and move 9 to the left:

Show the addition of 12 to -9. Start from the end of the previous arrow and move 12 to the right:

The final arrow is pointed at 3. This is the

3

Explained below.

Step-by-step explanation:

A two-sample test is to be performed to determine whether the mean weight loss for those on low-carbohydrate or Mediterranean diets is greater than the mean weight loss for those on a conventional low-fat diet.

(a)

The hypothesis can be defined as follows:

H₀: μ₁ - μ₂ ≤ 0 vs. Hₐ: μ₁ - μ₂ > 0

(b-1)

Use Excel to perform the t test for independent samples.

The output is attached below.

The test statistic value is, t = 7.58.

(b-2)

The degrees of freedom is, df = 58.

The critical value is, t₅₈ = 1.672.

The rejection region is:

Rejected H₀ if t > t₅₈ = 1.672.

(c)

Decision:

t = 7.58 > t₅₈ = 1.672

The null hypothesis will be rejected at 5% level of significance.

Thus, the nutritionist can conclude that overweight people on low-carbohydrate or Mediterranean diets lost more weight than people on a conventional low-fat diet.

The correct option is Yes.

Explained below.

Step-by-step explanation:

A two-sample test is to be performed to determine whether the mean weight loss for those on low-carbohydrate or Mediterranean diets is greater than the mean weight loss for those on a conventional low-fat diet.

(a)

The hypothesis can be defined as follows:

H₀: μ₁ - μ₂ ≤ 0 vs. Hₐ: μ₁ - μ₂ > 0

(b-1)

Use Excel to perform the t test for independent samples.

The output is attached below.

The test statistic value is, t = 7.58.

(b-2)

The degrees of freedom is, df = 58.

The critical value is, t₅₈ = 1.672.

The rejection region is:

Rejected H₀ if t > t₅₈ = 1.672.

(c)

Decision:

t = 7.58 > t₅₈ = 1.672

The null hypothesis will be rejected at 5% level of significance.

Thus, the nutritionist can conclude that overweight people on low-carbohydrate or Mediterranean diets lost more weight than people on a conventional low-fat diet.

The correct option is Yes.

12

Step-by-step explanation:

Left:

Simplify the following:

-9 - -12

-(-12) = 12:

-9 + 12

-9 + 12 = 3:

3

Right:

Do the following addition:

-9 + 12

The number -9 is negative. Start from 0 and move 9 to the left:

Show the addition of 12 to -9. Start from the end of the previous arrow and move 12 to the right:

The final arrow is pointed at 3. This is the

3

Step-by-step explanation:

a)

Here researcher claims that the mean weight loss for those on  low-carbohydrate or Mediterranean diets is greater than the mean  weight loss for those on a conventional low-fat diet

Set the null and alternative hypotheses to test the above claim as below.

versus

b)

Assume that the variance of the two populations are equal.

Under the null hypothesis, the test statistics is defined as

where

Use the foll owing Excel instructions and conduct the above test.

Step1: Enter the datainto two columns of spreadsheet.

Step2: Select Data Analysis from Data ribbon.

Step3: Select t-test. Two-sample Assuming equal variances.

Step4: Input the data range for variable 1 and variable 2.

Step5: Enter 0 as the Hypothesized Mean Difference.

Step6: Click OK.

Thus, the resultant outout is as follows:

                                                       Low-carb                        Low-fat

Mean                                               9.773333333       6.283333333

Variance                                          3.197885057                    3.160747126

Observations                                  30                                      30

Pooled Variance                             3.179316092

Hypothesized Mean Difference     0

df                                                      58

t Stat                                                 7.580610844

P(T < = t) one-tail                              1.54916E - 10

t Critical one — tail                           1.671552762

P(T <2) two-tail                                  3.09831E - 10

t Critical two - tail                              2.001717484

1) From the above output, the test statistics is obtained as t =  7.5806

2) From the above output, the critical value for one-tailed testis  obtained as

Rejection rule:  Reject if

c)

At 5% level of significance, the calculated value of test statistics  is greater than the critical value.

Therefore, reject the null hypothesis.

Hence, the nutritionist conclude that overweight people on  low-carbohydrate or Mediterranean diets lost more weight than  people on a conventional low-fat diet.

Step-by-step explanation:

Hello!

You have the information about voltage readings at an old and a new manufacturing location obtained remotely.

a, b and c in the attachment.

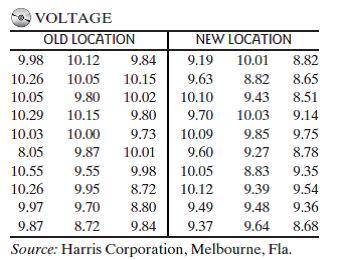
Histograms for a and c:

To construct a frequency histogram you have to first arrange the data for both locations in a frequency table. For this, I'm going to determine 5 class interval for each location. To do so you need to calculate the width of the intervals. First, you calculate the range of the variable and then you have to divide it by the number of intervals you want to do.

Old location: Range= 10,55-8,05= 2,5 → Class width: 2,5/5= 0,5

New Location: Range= 10,12-8,51= 1,61 → Class width: 1,61/5= 0,322

Starting from the minimum value you add the calculated width and create the intervals:

Old Location:

8,05-8,55

8,55-9,05

9,05-9,55

9,55-10,05

10,05-10,55

New Location

8,51-8,83

8,83-9,15

9,15-9,48

9,48-9,80

9,80-10,12

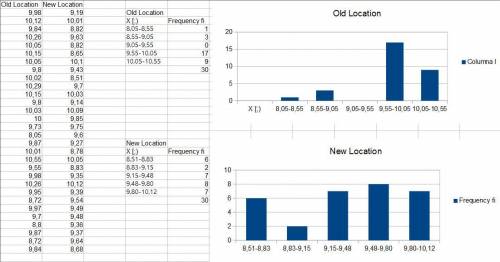
Stem and Leaf diagram for b:

To construct this diagram first I've ordered the data from leat to greatests. Then I've used the integer to form the stem 8,- 9.- and 10.- and the decimals are placed in the leafs of the diagram.

Comparing it to the histogram and stem and leaf diagram for the readings of the Old Location, the histogram stem, and leaf diagram show better where most of the readings lie.

d.

Comparing both histograms, it looks like the readings in the new location are more variable than the readings in the old location but more uniformly distributed. I would say that the readings in the new location are better than the readings in the old location.

e.

To calculate the mean you have to apply the following formula:

X[bar]= (∑xi'fi)/n

X[bar]OLD=(∑xi'fi)/n= (8.3*1+8.8*3+9.3*0+9.8*17+10.3*9)/30= 294/30= 9.8

X[bar]NEW=(∑xi'fi)/n= (8.67*6+8.99*2+9.315*7+9.64*8+9.96*7)/30= 282.045/30= 9.4015≅9.40

First you have to calculate the position of the median:

For both data sets the PosMe= 30/2=15

Now you arrange the data from least to highest and determine wich observation is in the 15th position:

Old Location

8,05 , 8,72 , 8,72 , 8,8 , 9,55 , 9,7 , 9,73 , 9,8 , 9,8 , 9,84 , 9,84 , 9,87 , 9,87 , 9,95 , 9,97 , 9,98 , 9,98 , 10 , 10,01 , 10,02 , 10,03 , 10,05 , 10,05 , 10,12 , 10,15 , 10,15 , 10,26 , 10,26 , 10,29 , 10,55

MeOLD= 9.97

New Location

8,51 , 8,65 , 8,68 , 8,78 , 8,82 , 8,82 , 8,83 , 9,14 , 9,19 , 9,27 , 9,35 , 9,36 , 9,37 , 9,39 , 9,43 , 9,48 , 9,49 , 9,54 , 9,6 , 9,63 , 9,64 , 9,7 , 9,75 , 9,85 , 10,01 , 10,03 , 10,05 , 10,09 , 10,1 , 10,12

MeNEW= 9.43

The mode is the observation with more absolute frequency.

To determine the mode on both data sets I'll use the followinf formula:

Md= Li + c [Δ₁/(Δ₁+Δ₂)]

Li= Lower bond of the interval with most absolute frequency (modal interval)

c= amplitude of the modal interval

Δ₁= absolute frequency of the modal interval minus abolute frequency of the previous interval

Δ₂= absolute frequency of the modal interval minus the absolute frequency of the next interval

Modal interval OLD

9,55-10,05

Δ₁= 17-0= 17

Δ₂= 17-9= 8

c= 0.5

Li= 9.55

MdOLD= 9.55 + 0.5*[17/(17+8)]= 9.89

Modal interval NEW

9,48-9,80

Δ₁= 8-7= 1

Δ₂= 8-7= 1

c= 0.32

Li= 9.48

MdNEW= 9.48+0.32*[1/(1+1)]= 9.64

f.

OLD

Mean 9.8

SE 0.45

X= 10.50

Z= (10.50-9.8)/0.45= 1.56

g.

NEW

Mean 9.4

SE 0.48

X=10.50

Z= (10.50-9.4)/0.48=2.29

h. The Z score for the reading 10.50 for the old location is less than the Z score for the reading 10.50 for the new location, this means that the reading is closer to the mean in the old location than in the new location.

The reading 10.50 is more unusual for the new location.

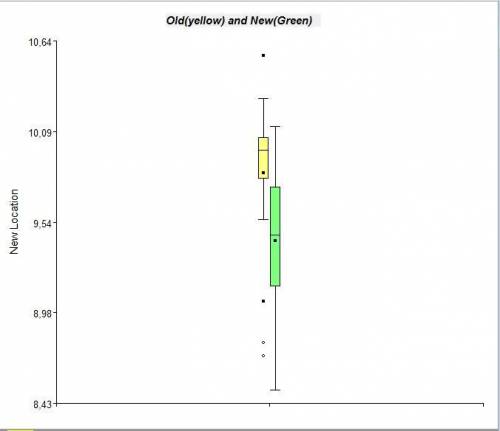
i. and k. Boxplots attached.

There are outliers for the readings in the old location, none in the readings for the new location.

j. To detect outliers using the Z- score you have to "standardize every value of the data set using the corresponding values of the mean and standard deviation. Observations that obtained a Z-score greater than 3 or less than -3 are outliers.

The data set for the new location has no outliers, To prove it I've calculated the Z-scores for the max and min values:

Min: Z=(8.51-9.4)/0.48= -1.85

Max: Z=(10.12-9.4)/0.48= 1.5

The records for the old location show, as seen in the boxplot, outliers:

To find them I'll start calculating values of Z from the bottom and the top of the list until getting a value Z≥-3 and Z≤3

Bottom:

1) 8,05 ⇒ Z=(8.05-9.8)/0.45= -3.89

2) 8,72 ⇒ Z= (8.72-9.8)/0.45= -2.4

Top

1) 10,55⇒ Z= (10.55-9.8)/0.45= 1.67

m. As mentioned before, the distribution for the new location seems to be more uniform and better distributed than the distribution for the old location. Both distributions are left-skewed, the distribution for the data of the old location is severely affected by the presence of outliers.

I hope this helps!

Yes , there is evidence that the average EER is different from 9.0

Step-by-step explanation:

Summing up the samples given , we have 331.6

Therefore , sample mean = 331.6/36

≈9.2

The standard deviation is ≈ 0.38

Since n > 30 , then we use  Z- statistics

Let : Average EER = 9

: Average ≠ 9

using the z - formula

z =

=

= 3. 15

Checking the z- value at 0.05 , we have 1.64

Conclusion: since the z- calculate value is greater than the z-tab , then we reject the null hypothesis and conclude that there the average EER is different from 9