Mathematics : asked on jenna34032

29.07.2022

Rotate the figure 90 degrees clockwise then translate 4 units left

0

Step-by-step answer

09.07.2023, solved by verified expert

Mathematics, English, Physics. Research Scholar at Indian Institute of Technology, Roorkee

5 316 answers

Unlock the full answer

If I am not mistaken, the new figure will be here (view attachment, bright blue figure is the new transformation)

Rotate the figure 90 degrees clockwise then translate, №18011253, 29.07.2022 11:58

It is was helpful?

Helpful Useless

Faq

Mathematics

Rotate the figure 90 degrees clockwise then translate 4 units left

Step-by-step answer

P Answered by Master

If I am not mistaken, the new figure will be here (view attachment, bright blue figure is the new transformation)

Rotate the figure 90 degrees clockwise then translate 4 units left

Mathematics

What are two possible transformations that together could have been used to create the red figure from the blue figure? a) a reflection across the x axis followed by a reflection across the y axis b) a translation of 1 unit down followed by a rotation of 90 degrees clockwise about the origin c) a rotation of 90 degrees counterclockwise about the origin followed by a reflection across the x axis d) a rotation of 90 degrees counterclockwise about the origin followed by a translation of 1 unit down

Step-by-step answer

P Answered by Specialist

4

I think its either C or D give me one second to figure it out.

Mathematics

What are two possible transformations that together could have been used to create the red figure from the blue figure? a) a reflection across the x axis followed by a reflection across the y axis b) a translation of 1 unit down followed by a rotation of 90 degrees clockwise about the origin c) a rotation of 90 degrees counterclockwise about the origin followed by a reflection across the x axis d) a rotation of 90 degrees counterclockwise about the origin followed by a translation of 1 unit down

Step-by-step answer

P Answered by Master

4

I think its either C or D give me one second to figure it out.

Mathematics

Which sequence of transformations produces an image that is not congruent to the original figure? a. a translation of 4 units to the right followed by a dilation of 2. b. a rotation of 90 degrees clockwise followed by a translation of 2 units to the left. c. a translation of 3 units to the left followed by a reflection across the y-axis. d. a reflection across the y-axis followed by a rotation of 90 degrees counterclockwise.

Step-by-step answer

P Answered by PhD

117

The correct answer is:

A) A translation of 4 units to the right followed by a dilation of 2.

Explanation:

3 of our transformations are called isometries. These are transformations that preserve the size and shape of the original figure; they just change the position or orientation of it. Translations, reflections and rotations are all isometries. We know that isometries preserve congruence, since they maintain the size and shape of the original figure.

A dilation is not an isometry. This is because a dilation changes the size of a figure. Since the new figure will not be the same size as the original, they will not be congruent.

Mathematics

Which sequence of transformations produces an image that is not congruent to the original figure? a. a translation of 4 units to the right followed by a dilation of 2. b. a rotation of 90 degrees clockwise followed by a translation of 2 units to the left. c. a translation of 3 units to the left followed by a reflection across the y-axis. d. a reflection across the y-axis followed by a rotation of 90 degrees counterclockwise.

Step-by-step answer

P Answered by PhD

117

The correct answer is:

A) A translation of 4 units to the right followed by a dilation of 2.

Explanation:

3 of our transformations are called isometries. These are transformations that preserve the size and shape of the original figure; they just change the position or orientation of it. Translations, reflections and rotations are all isometries. We know that isometries preserve congruence, since they maintain the size and shape of the original figure.

A dilation is not an isometry. This is because a dilation changes the size of a figure. Since the new figure will not be the same size as the original, they will not be congruent.

Mathematics

Which transformations will produce similar, but not congruent figures? a.) triangle mno is reflected across the x-axis and then rotated 90 degrees clockwise to form triangle m n o . b.) triangle mno is reflected across the x-axis and then translated 9 units down to form triangle m n o . c.) triangle mno is reflected across the y-axis and then dilated by a scale factor of 1.8 to form triangle m n o . d.) triangle mno is reflected across the y-axis and then rotated 180 degrees clockwise to form triangle m n o .

Step-by-step answer

P Answered by PhD

79

If you rotate, translate, or reflect a figure, the afterimage will be congruent to the original.
But if you dilate the figure, you are changing the dimensions and the length of its sides. However, angle measures are preserved and therefore that makes the figure and its afterimage similar.
Therefore C.) produces a similar but not congruent figure because there is the dilation in it.

Mathematics

Which transformations will produce similar, but not congruent figures? a.) triangle mno is reflected across the x-axis and then rotated 90 degrees clockwise to form triangle m n o . b.) triangle mno is reflected across the x-axis and then translated 9 units down to form triangle m n o . c.) triangle mno is reflected across the y-axis and then dilated by a scale factor of 1.8 to form triangle m n o . d.) triangle mno is reflected across the y-axis and then rotated 180 degrees clockwise to form triangle m n o .

Step-by-step answer

P Answered by PhD

79

If you rotate, translate, or reflect a figure, the afterimage will be congruent to the original.
But if you dilate the figure, you are changing the dimensions and the length of its sides. However, angle measures are preserved and therefore that makes the figure and its afterimage similar.
Therefore C.) produces a similar but not congruent figure because there is the dilation in it.

Mathematics

A parallelogram with coordinates A (-2,3), B (3,3), C (4,6), and D(-1,6) is the first rotated 90 degrees clockwise and then translated 4 units left and 2 units down to form quadrilateral A B C D what is the distance, in units between point C and point D in the resulting figure

Step-by-step answer

P Answered by PhD

14

Given:

The vertices of a parallelogram are A (-2,3), B (3,3), C (4,6), and D(-1,6).

It is first rotated 90 degrees clockwise and then translated 4 units left and 2 units down to form quadrilateral A'B'C'D.

To find:

The distance between C' and D'.

Solution:

If a figure rotated 90 degrees clockwise, then

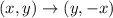
$(x,y)\to (y,-x)$

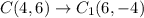
$C(4,6)\to C_1(6,-4)$

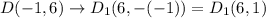
$D(-1,6)\to D_1(6,-(-1))=D_1(6,1)$

If figure translated 4 units left and 2 units down, then

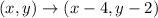
$(x,y)\to (x-4,y-2)$

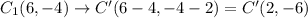
$C_1(6,-4)\to C'(6-4,-4-2)=C'(2,-6)$

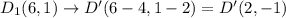
$D_1(6,1)\to D'(6-4,1-2)=D'(2,-1)$

Distance formula:

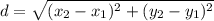
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$

Distance between C'(2,-6) and D'(2,-1) is

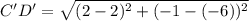
$C'D'=\sqrt{(2-2)^2+(-1-(-6))^2}$

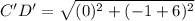
$C'D'=\sqrt{(0)^2+(-1+6)^2}$

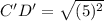
$C'D'=\sqrt{(5)^2}$

C'D'=5

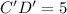
Therefore, the distance between C'D' is 5 units.

Mathematics

Carmen performed two transformations on the blue figure. what transformations did she perform to get the red figure? a) a reflection across the y axis followed by a reflection across the x axis b) a translation of 5 units right and 1 unit down followed by a reflection across the x axis c) a reflection across the x axis followed by a reflection across the y axis d) a translation of 5 units right and 1 unit down followed by a rotation of 90 degrees clockwise about the origin

Step-by-step answer

P Answered by PhD

6

B) a translation of 5 units right and 1 unit down followed by a reflection across the x axis

Mathematics

Carmen performed two transformations on the blue figure. what transformations did she perform to get the red figure? a) a reflection across the y axis followed by a reflection across the x axis b) a translation of 5 units right and 1 unit down followed by a reflection across the x axis c) a reflection across the x axis followed by a reflection across the y axis d) a translation of 5 units right and 1 unit down followed by a rotation of 90 degrees clockwise about the origin

Step-by-step answer

P Answered by PhD

6

B) a translation of 5 units right and 1 unit down followed by a reflection across the x axis

free Ask question

Today we have helped

412 students

just now

Business

You're prepared to make monthly payments of $310, beginning at the end of this month, into an account that pays 4 percent interest compounded monthly. How many payments will you have made when your account balance reaches $20,175

p Answered by PhD

just now

Mathematics

A real estate agent gets a 5.5% commission on all of the houses she sells How much money would she make for selling a $198,000 house

p Answered by PhD

just now

Business

Which of the following statements is an example of a personal skill: a. I volunteer in my community

b. I’m a really good cook

c. I like being outside

d. I love learning new things

p Answered by PhD

1 minute ago

Mathematics

Amanda has a piece of ribbon that is 1/4 had long. She wants to share the ribbon with 2 friends so that they can each wear a ribbon for breast cancer awareness month. If each of the 3 friends gets the same amount, how much ribbon will each person get?

m Answered by Master

1 minute ago

Mathematics

What is 5x - 3y when x equals negative 2 and Y equals 6

p Answered by PhD

Get help with homework

What is Studen

Studen helps you with homework in two ways:

Our base includes complete solutions from various experts

chat

Leave a question

Studen will automatically choose an expert for you.

directly

We have more than 5 000 verified experienced expert