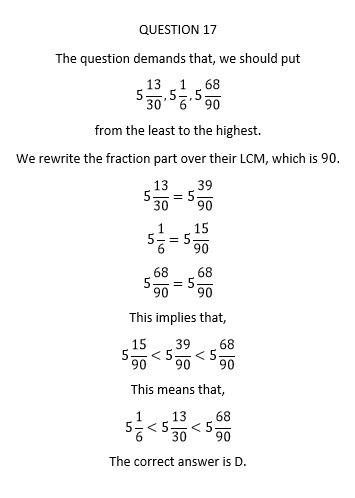QUESTION 1
We want to find the digit that should fill the blank space to make
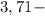
divisible by 9.
If a number is divisible by 9 then the sum of the digits should be a multiple of 9.
The sum of the given digits is,
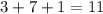
Since
which is a multiple of 9.
This means that
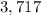
is divisible by 9.
The correct answer is B
QUESTION 2
The factors of the number 30 are all the numbers that divides 30 exactly without a remainder.
These numbers are ;
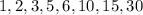
The correct answer is A.
QUESTION 3.
We want to find the prime factorization of the number 168.
The prime numbers that are factors of 168 are
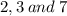
We can write 168 as the product of these three prime numbers to obtain,
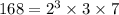
We can also use the factor tree as shown in the attachment to write the prime factorization of 168 as
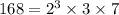
The correct answer is B.
QUESTION 4.
We want to find the greatest common factor of
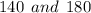
We need to express each of these numbers as a product of prime factors.
The prime factorization of 140 is
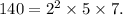
The prime factorization of 180 is
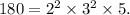
The greatest common factor is the product of the least degree of each common factor.
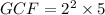
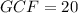
The correct answer is A.
QUESTION 5.
We want to find the greatest common factor of
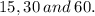
We need to first find the prime factorization of each number.
The prime factorization of 15 is
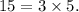
The prime factorization of 30 is
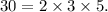
The prime factorization of 60 is
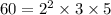
The greatest common factor of these three numbers is the product of the factors with the least degree that is common to them.
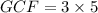
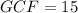
The correct answer is C.
QUESTION 6
We want to determine which of the given fractions is equivalent to
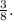
We must therefore simplify each option,
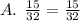
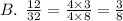
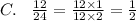
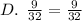
The simplification shows that
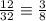
The correct answer is B.
QUESTION 7.
We want to express
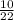
in the simplest form.
We just have to cancel out common factors as follows.
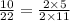
This simplifies to,
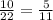
The correct answer is C.
QUESTION 8.
We were given that Justin visited 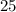 of the
of the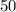 states.
states.
The question requires that we express 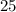 as a fraction of
as a fraction of 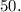
This will give us
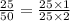
We must cancel out the common factors to have our fraction in the simplest form.
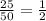
The correct answer is C.
QUESTION 9.
We want to write
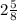
as an improper fraction.
We need to multiply the 2 by the denominator which is 8 and add the product to 5 and then express the result over 8.
This gives us,
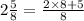
this implies that,
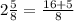
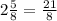
Sarah needed
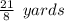
The correct answer is D.
QUESTION 10
See attachment
QUESTION 11
We wan to write
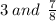
as an improper fraction.
This implies that,
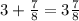
To write this as a mixed number, we have,
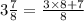
This implies that,
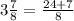
This gives
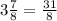
The correct answer is B.
QUESTION 12
We want to find the LCM of 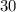 and
and 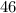 using prime factorization.
using prime factorization.
The prime factorization of 30 is 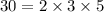
The prime factorization of 46 is 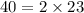 .
.
The LCM is the product of the common factors with the highest degrees. This gives us,
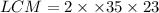
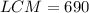
The correct answer is D.
QUESTION 13
We want to find the least common multiple of 3,6 and 7.
The prime factorization of 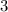 is
is 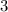 .
.
The prime factorization of 6 is 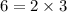 .
.
The prime factorization of 7 is 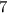 .
.
The LCM is the product of the common factors with the highest degrees. This gives us,
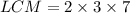
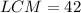 .
.
The LCM is 42, therefore 42 days will pass before all three bikes will at the park on the same day again.
The correct answer is B.
See attachment for continuation.