1). Slope = 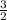
2). Slope = 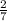
3). Slope = 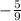
4). Option A. 2x + 4
5). Option C. 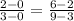
Step-by-step explanation:
1). Slope of a line segment EF with E(-2, -4) and F(2, 2)
Slope m = 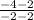
m = 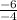
m = 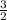
2). Slope of a line segment AD with A(-3, -2) and D(4, 0)
Slope m = 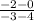
m = 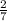
3). Slope of a line JK with J(-4, 2) and K(5, -3)
m = 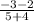
m = 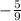
4). We have to determine the equation of the line given by graph.
In other words we have to determine the eequation of a line passing through (0, 4) and (-2, 0)
Equation will be in the form of y = mx + c
Where c = y-intercept = 4 units
Slope m = 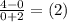
Therefore, equation of the line will be y = 2x + 4
Option A. 2x + 4 is the answer.
5). If triangles ABC and CFG are similar then AC and CG will have same slope.
Slope of AC with A(0,0) and C(3, 2) = Slope of CG with C(3, 2) and G(9, 6)
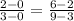
Therefore, Option C. is the correct option.