11. Ans: (D)
Since all the vertices and the foci lie along the y axis, therefore, we would need the following equation for vertical hyperbola:
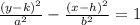
Since (h,k) = (0,0)
Therefore, the above equation becomes,
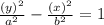
Now the distance between the vertices is:
2a = 12
=> a = 6
And the distance between the foci is:
2c = 18
=> c = 9
Since,
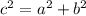
=>
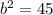
Hence, the equation becomes,
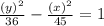
(Option D:y squared over 36 minus x squared over 45 = 1)
12. Ans: (B)
The hyperbola's standard form is(as it is a vertical):
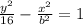
-- (X)
=>
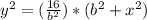
=> y = ±
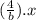
--- (A)
Since asymptotes at y = ±
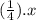
. --- (B)
Compare (A) and (B), you would get,
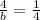
=> b=16
The equation (X) would become:
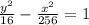
(Option-B)
13. Ans: (A)
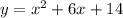
Equations given:
x = t - 3 --- (equation-1)
y =
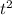
+ 5 --- (equation-2)
From equation-1,
t = x + 3
Put the value of t in (equation-2),
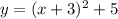
Hence, the correct option is (A)
14. Ans: (A)
The polar coordinates given:
= (r, θ)
Since,
x = r*cosθ,
y = r*sinθ
Plug-in the values of r, and θ in the above equations:
x = (3) * cos(120°); since
= 120°
=> x =
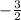
y = (3) * sin(120°);
=> y =
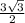
Ans: (x,y) =
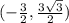
(Option A)
15. Ans: (D)
The general forms of finding all the polar coordinates are:
1) When r >= 0(meaning positive): (r, θ + 2n
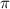
) where, n = integer
2) When r < 0(meaning negative): (-r, θ + (2n+1)
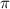
) where, n = integer
Since r is not mentioned in the question, but in options every r slot has the value r=1, therefore, I would take r = +1, -1(plus minus 1)
θ(given) =
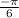
When r = +1(r>0):
(1,
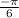
+ 2n
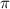
)
When r = -1(r<0):
(-1,
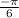
+ (2n+1)
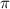
)
Therefore, the correct option is (D): (1, negative pi divided by 6 + 2nπ) or (-1, negative pi divided by 6 + (2n + 1)π)
16. Ans: (B)
In polar coordinates,
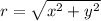
Since x = 4, y=4; therefore,
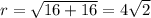
To find the angle,
tanθ = y/x = 4/4 = 1
=> θ = 45° (when
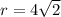
)
If r = -
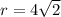
, then,
θ = 45° + 180° = 225°
Therefore, the correct option is (B) (4 square root 2 , 45°), (-4 square root 2 , 225°)
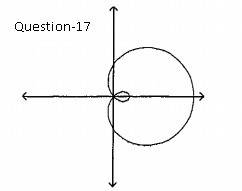
17. Ans: (B)
(Question-17 missing Image is attached below) The general form of the limacon curve is:
r = b + a cosθ
If b < a, the curve would have inner loop. As you can see in the image attached(labeled Question-17), the limacon curve graph has the inner loop. Therefore, the correct option is (B) r = 2 + 3 cosθ, since b = 2, and a = 3; and the condition b < a (2 < 3) is met.
18. Ans: (C)
Let's find out!
1. If we replace θ with -θ, we would get:
r = -2 + 3*cos(-θ )
Since, cos(-θ) = +cosθ, therefore,
r = -2 + 3*cos(θ)
Same as the original, therefore, graph is symmetric to x-axis.
2. If we replace r with -r, we would get:
-r = -2 + 3*cos(θ )
r = 2 - 3*cos(θ)
NOT same as original, therefore, graph is NOT symmetric to its origin.
3. If we replace θ with -θ and r with -r, we would get:
-r = -2 + 3*cos(-θ )
Since, cos(-θ) = +cosθ, therefore,
r = 2 - 3*cos(3θ)
NOT same as original, therefore, graph is NOT symmetric to y-axis.
Ans: The graph is symmetric to: x-axis only!
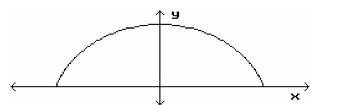
19. (Image is attached below) As the question suggests that it is a horizontal ellipse, therefore, the equation for the horizontal ellipse is:
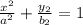
-- (A)
Since, x = 8f,
y = 18ft,
b = 54ft,
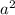
= ?
Plug-in the values in equation (A),
(A)=>
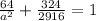
=>
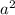
= 72
Therefore, the equation becomes,
Ans:
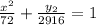
20. Ans: x-axis only
Let's find out!
1. If we replace θ with -θ, we would get:
r = 2*cos(-3θ )
Since, cos(-θ) = +cosθ, therefore,
r = +2*cos(3θ) = Same as original
Therefore, graph is symmetric to x-axis.
2. If we replace r with -r, we would get:
-r = 2*cos(3θ )
r = -2*cos(3θ) = Not same
3. If we replace θ with -θ and r with -r, we would get:
-r = 2*cos(-3θ )
Since, cos(-θ) = +cosθ, therefore,
r = -2*cos(3θ) = Not Same
Ans: The graph is symmetric to: x-axis only!