a) The error is that, the initial value is n=1 NOT n=3
b) The sum is 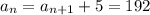
c)The explicit formula is 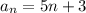
The recursive formula is 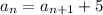 ,
,
Step-by-step explanation:
The given arithmetic series is 8 + 13 + ... + 43.
The first term is 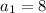 , the common difference is
, the common difference is 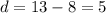
The nth term is given by:
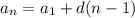
We substitute the values to get:
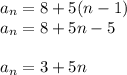
To find how many terms are in the sequence we solve the equation:
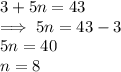
The summation notation is 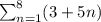
The error the student made is in the initial value.
It should be n=1 NOT n=3
b) The sum of the arithmetic series is calculated using:
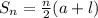
We substitute o get:
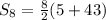
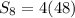
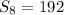
c) The explicit formula we already calculated in a), which is 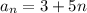
The recursive formula is given as:
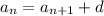
We substitute d=5 to get:
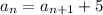
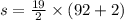 That's ur answer :)
That's ur answer :)