0The transformations that are needed to change the parent cosine function to y = 0.35×cos(8(x-π/4)) are:
vertical stretch of 0.35horizontal compression of period of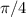
phase shift of 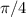to rightHow does transformation of a function happens?The transformation of a function may involve any change.
Usually, these can be shift horizontally (by transforming inputs) or vertically (by transforming output), stretching (multiplying outputs or inputs) etc.
If the original function is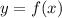 
, assuming horizontal axis is input axis and vertical is for outputs, then:
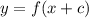earlier)Right shift by c units: 
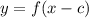output, but c units late)Vertical shift:Up by d units: 
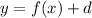Down by d units: 
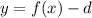Stretching:Vertical stretch by a factor k: 
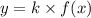Horizontal stretch by a factor k: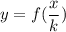 
For this case, we're specified that:
y = cos(x) (the parent cosine function) was transformed to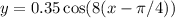 
We can see its vertical stretch by 0.35, right shift by 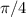horizontal stretch by 1/8
Period of cos(x) is of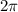 
length. But 1.8 stretching makes its period shrink to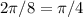 
Thus, the transformations that are needed to change the parent cosine function to y = 0.35×cos(8(x-π/4)) are:
vertical stretch of 0.35horizontal compression to period of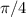 (which means period of cosine is shrunk to 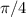which originally was 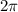)phase shift of 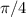to rightLearn more about transformation of functions here:
4 281
rating
Get help with homework
