1. y varies directly with x and the equation is 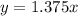
2. No, y does not vary directly with x
3. Your car travels 58 miles in 1 hour
4. 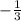
4. 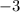
5. 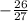
6. 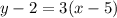
7. 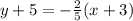
8. 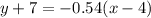
9. 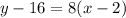
10. 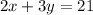
11. 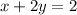
Step-by-step explanation:
1.
For 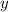 to vary directly with
to vary directly with  , all the 3 pair of numbers need to show the same ratio if we divide each y's by the x's. Let's check.
, all the 3 pair of numbers need to show the same ratio if we divide each y's by the x's. Let's check.
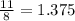
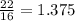
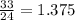
So all of them show the same ratio and hence y varies directly with x.
For equation, we already saw that multiplying x by 1.375 gives us y. We can write in equation form as:
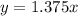
Third answer choice is correct.
2.
This is similar to #1. So let's check the ratios.
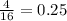
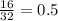
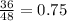
As we can see, the ratios are not equal to y does not vary directly with x.
Fourth answer choice is correct.
3.
The first number in the pair gives time and second number gives distance. To get unit rate, we divide the distance by time. So we will get the number of miles traveled in 1 hour.
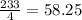 [ i believe this is a typo and it should be 232 miles and ratio would be 58 ]
[ i believe this is a typo and it should be 232 miles and ratio would be 58 ]
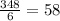
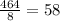
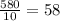
As we can see, in 1 hour, distance covered is 58 miles. Third answer choice is right.
4.
If the 2 points are taken as 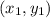 and
and 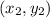
And we know formula of slope to be:
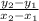
The slope of the line is:
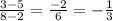
The slope of the line is 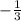
Second answer choice is correct.
4. [this should be #5]
If the 2 points are taken as 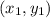 and
and 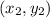
And we know formula of slope to be:
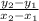
The slope of this line can be found now:
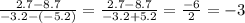
The slope of the line is 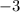
Fourth answer choice is correct.
5.
The formula of slope is:
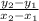
Where,
the 2 points are taken as 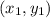 and
and 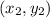
Now finding the slope:
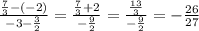
The slope of the line is 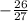
Second answer choice is right.
6.
Point Slope form of a line is given as:
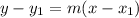
Where,
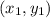
is the point given, andm is the slope
Using the point (5, 2) and slope as 3 given, we can write the equation:
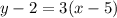
Fourth answer choice is right.
7.
Point Slope form of a line is given as:
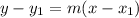
Where,
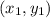
is the point given, andm is the slope
Using the point given as 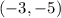 and slope as
and slope as 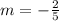 , we can write the point slope form of the equation as:
, we can write the point slope form of the equation as:
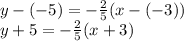
First answer choice is right.
8.
Point Slope form of a line is given as:
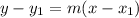
Where,
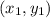
is the point given, andm is the slope
The slope is given as 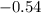 and the point is (4, -7). So the point slope form is:
and the point is (4, -7). So the point slope form is:
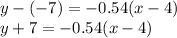
First answer choice is right.
9.
In this question, we can just have a quick look and see that the 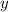 -coordinate is 8 times the
-coordinate is 8 times the  -coordinate. So we can say that
-coordinate. So we can say that 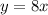
Expanding the equations below would tell us which one is equal to that. Let's check.
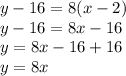
This is the correct one.
So first answer choice is right.
10.
The standard form of the equation of a line is given as:
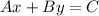
Rearranging the given equation gives us:
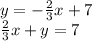
Now, we can't have a fraction, so we multiply all of it by 3 to get rid of the denominator. Now we have:
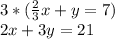
First answer choice is right.
11.
The standard form of a line is 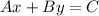
Rearranging the given equation, we have:
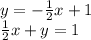
We cannot have fractions, so we multiply the whole thing by 2 to get rid of the denominator. So we have:
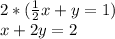
First answer choice is correct.
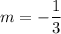 The lines passes through the point (3,5)
The lines passes through the point (3,5)