A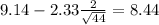 gas at 8.4 atm has a volume of 1.9 L. What, №17887886, 03.11.2021 07:31

Physics

A gas at 8.4 atm has a volume of 1.9 L. What volume would the gas have at 8.3 atm?

Step-by-step answer

P Answered by PhD

1

the final volume of the gas is 1.923 L.

Explanation:

Given;

initial pressure, P₁ = 8.4 atm

initial volume of the gas, V₁ = 1.9 L

final pressure of the gas, P₂ = 8.3 atm

The final volume of the gas is calculated by applying Boyle's law as follows;

P₁V₁ = P₂V₂

V₂ = P₁V₁ / P₂

V₂ = (8.4 x 1.9) / 8.3

V₂ = 1.923 L

Therefore, the final volume of the gas is 1.923 L.

Chemistry

How many liters of 1.5 m hcl solution would react completely with 6.5 moles ca(oh)2? ca(oh)2(s) + 2 hcl(aq) yields cacl2(aq) + 2 h2o(l) 2.2 l hcl(aq) 4.9 l hcl(aq) 8.7 l hcl(aq) 1.9 l hcl(aq)

Step-by-step answer

P Answered by Specialist

4

First, multiply the 6.5 moles by the mole ratio of 2/1, which yields 13 moles of HCL. Then, divide 13/1.5, which yields an answer of 8.7 L HCL(aq), or C.

Hope this helps!

Chemistry

How many liters of 1.5 m hcl solution would react completely with 6.5 moles ca(oh)2? ca(oh)2(s) + 2 hcl(aq) yields cacl2(aq) + 2 h2o(l) 2.2 l hcl(aq) 4.9 l hcl(aq) 8.7 l hcl(aq) 1.9 l hcl(aq)

Step-by-step answer

P Answered by Master

4

First, multiply the 6.5 moles by the mole ratio of 2/1, which yields 13 moles of HCL. Then, divide 13/1.5, which yields an answer of 8.7 L HCL(aq), or C.

Hope this helps!

Mathematics

Drag the amounts to order them from greatest to least. 1 qt ≈ 0.95 l 1 gal = 4 qt 1 qt = 2 pt 1. 9 l 3.8 pt 0.6 gal

Step-by-step answer

P Answered by Specialist

30

1. 9 L
2. 0.6 gal
3. 3.8 pt

Mathematics

Drag the amounts to order them from greatest to least. 1 qt ≈ 0.95 l 1 gal = 4 qt 1 qt = 2 pt 1. 9 l 3.8 pt 0.6 gal

Step-by-step answer

P Answered by Specialist

30

1. 9 L
2. 0.6 gal
3. 3.8 pt

French

I WILL MARK BRAINLIEST PLEASE Fill in the blanks in the following sentences with the correct passé composé form of the verb in parentheses. 1. Elle de bonne heure ce matin. (se lever) 2. Ils à Paris en train. (arriver) 3. Tu un plat regional. (déguster) 4. Vous les mains à quelle heure? (se laver) Fill in the blanks in the following sentences with the appropriate animal nouns. Remember to include the appropriate definite articles. 5. La femelle du cheval est . 6. Le mâle de la poule est . Fill in the blanks in the following sentences with the appropriate

Step-by-step answer

P Answered by PhD

11

Bonjour,

1. Elle "s'est levée" de bonne heure ce matin. (se lever)

2. Ils "sont arrivés" à Paris en train. (arriver)

3. Tu "as dégusté" un plat regional. (déguster)

4. Vous "vous êtes lavés" les mains à quelle heure? (se laver)

5. La femelle du cheval est "la jument".

6. Le mâle de la poule est "le coq".

7. Dans "le verger" , il y a beaucoup de fruits dans les arbres.

8. Le peintre a exposé "les tableaux" dans la galerie.

9. L'ouest de la France est bordé par " la mer" Atlantique.

10. Il est mal signifie Il est mal habillé.

14. Est-ce que tu as assez de soupe?

Oui, j'en ai assez.

15. Combien de baguettes est-ce que vous allez prendre? (Two)

Nous allons en prendre deux.

16. Dans la salle de bains, on se lave les mains dans "un lavabo".

17. Dans la cuisine, je fais la vaisselle avec "une éponge".

18. On utilise pour faire la lessive.

19. Dans le salon, on s'assoit sur "un canapé".

20. Dans la salle à manger, je nettoie le sol avec "une serpillière".

French

I WILL MARK BRAINLIEST PLEASE Fill in the blanks in the following sentences with the correct passé composé form of the verb in parentheses. 1. Elle de bonne heure ce matin. (se lever) 2. Ils à Paris en train. (arriver) 3. Tu un plat regional. (déguster) 4. Vous les mains à quelle heure? (se laver) Fill in the blanks in the following sentences with the appropriate animal nouns. Remember to include the appropriate definite articles. 5. La femelle du cheval est . 6. Le mâle de la poule est . Fill in the blanks in the following sentences with the appropriate

Step-by-step answer

P Answered by PhD

11

Bonjour,

1. Elle "s'est levée" de bonne heure ce matin. (se lever)

2. Ils "sont arrivés" à Paris en train. (arriver)

3. Tu "as dégusté" un plat regional. (déguster)

4. Vous "vous êtes lavés" les mains à quelle heure? (se laver)

5. La femelle du cheval est "la jument".

6. Le mâle de la poule est "le coq".

7. Dans "le verger" , il y a beaucoup de fruits dans les arbres.

8. Le peintre a exposé "les tableaux" dans la galerie.

9. L'ouest de la France est bordé par " la mer" Atlantique.

10. Il est mal signifie Il est mal habillé.

14. Est-ce que tu as assez de soupe?

Oui, j'en ai assez.

15. Combien de baguettes est-ce que vous allez prendre? (Two)

Nous allons en prendre deux.

16. Dans la salle de bains, on se lave les mains dans "un lavabo".

17. Dans la cuisine, je fais la vaisselle avec "une éponge".

18. On utilise pour faire la lessive.

19. Dans le salon, on s'assoit sur "un canapé".

20. Dans la salle à manger, je nettoie le sol avec "une serpillière".

Mathematics

1. the width w of a rectangular swimming pool is x+4. the area a of the pool is 2x^3-29+12. what is an expression for the length of the pool? a. 2x^2+8x+3 b. 2x^2-8x-3 c. 2x^2-8x+3 d. 2x^2+8-3 2. simplify x/6x-x^2 a. 1/6-x; where x = 0,6 b. 1/6-x; where x=6 c. 1/6; where x=0 d. 1/6 3. simplify -12x4/x4+8x^5 a. -12/1+8x; where x= -1/8 b. -12/1+8x; where x= -1/8,0 4. simplify x+5/ x^2+6x+5 a. 1/x+1; where x= -1 b. 1/x+1; where x=-1, -5 5. simplify x^2-3x-18/x+3 a. x-3 b. x-6; where x= -3 c. x-6; where x= 6 d. 1/x+3; where x= -3 6. simplify 2/3a .

Step-by-step answer

P Answered by PhD

20

Question 1

To find the width of the rectangle, we divide the area by the length
$2x^{3}-29x+12$ ÷ x+4

We use the method of long division to get the answer. The method is shown in the first diagram below

$2x^{2}-8x+3$

Question 2:
$\frac{x}{6x-x^{2} } = \frac{x}{x(6-x)} = \frac{1}{6-x}$

Question 3:
$\frac{-12 x^{4} }{x^{4}+8 x^{5} }= \frac{-12 x^{4} }{ x^{4}(1+8x)}= \frac{-12}{1+8x}$

Question 4:
$\frac{x+5}{x^{2}+6x+5}= \frac{x+5}{(x+1)(x+5)}= \frac{1}{x+1}$

Question 5:
$\frac{x^{2}-3x-18} {x+3}= \frac{(x-6)(x+3)}{x+3}= \frac{x-6}{1}=x-6$

Question 6:
$\frac{2}{3a}$ × $\frac{2}{a^{2}}$ = $\frac{4}{3a^{3} }$ where $a \neq 0$

Question 7: (Question is not written well)
$\frac{x-5}{4x+8}$ × $(12x^{2}+32x+8)$
$\frac{12 x^{3}-28 x^{2} -152x-40 }{4x+8}$
By performing long division we get an answer $3 x^{2} -x-36$ with remainder of 248

Question 8:
$( \frac{x^{2}-16} {x-1})$ ÷ (x+4)

$( \frac{ x^{2}-16 }{x-1})$ × $\frac{1}{x+4}$
$\frac{(x+4)(x-1)}{x-1}$ × $\frac{1}{x+4}$
Cancelling out x+4

we obtain $\frac{x+1}{x-1}$

Question 9:
$\frac{x^{2}+2x+1} {x-2}$ ÷ $\frac{x^{2-1} }{x^{2}-4 }$
$\frac{ x^{2}+2x+1 }{x-2}$ × $\frac{x^{2}-4 }{x^{2}-1}$
Factorise all the quadratic expression gives
$\frac{(x+1)(x+1)}{x-2}$ × $\frac{(x-2)(x+2)}{(x+1)(x-1)}$
Cancelling out (x+1)

and

gives a simplest form
$\frac{(x+1)(x+2)}{x-1}$

Question 10:

$\frac{24 w^{10}+8w^{12} }{4 x^{4} }= \frac{24w^{10} }{4 x^{4} } + \frac{8 w^{12} }{4 x^{4} }$
Cancelling out the constants of each fraction
$\frac{6w^{10} }{x^{4} }+ \frac{2w^{12} }{x^{4}}= \frac{6w^{10}+2w^{12} }{ x^{4}}$

Question 11:

$\frac{-6m^{9}-6m^{8}-16m^{6} }{2m^{3} } = \frac{-2m^{6}(3m^{3}-3m^{2}-8)}{2m^{3} }$
Cancelling $2m^{3}$ gives us the simplified form
$-m^{3}(3m^{3}-3m^{2}-8) = -3m^{6}+3m^{5}+8m^{3}$

Question 12:

$\frac{-4x}{x+7} - \frac{8}{x-7} = \frac{-4x(x-7)-8(x+7)}{(x+7)(x-7)}$
$\frac{-4 x^{2} +28x-8x-56}{(x+7)(X-7)}= \frac{-4 x^{2} +20x-56}{(x+7)(x-7)}$
Factorising the numerator expression
$\frac{(-4x+28)(x-2)}{(x+7)(x-7)} = \frac{-4(x-7)(x-2)}{(x+7)(x-7)}$
Cancelling out x-7

gives the simplified form
$\frac{-4x+8}{x-7}$

Question 13:

$\frac{3}{x-3} - \frac{5}{x-2}= \frac{x3(x-2)-5(x-2)}{y(x-3)(x-2)}$
$\frac{3x-6-5x+15}{(x-3)(x-2)}= \frac{-2x+9}{(x-3)(x-2)}$

Question 14:

$\frac{9}{x-1}- \frac{5}{x+4}= \frac{9(x+4)-5(x-1)}{(x-1)(x+4)}$ $\frac{9x+36-5x+5}{(x-1)(x+4)}= \frac{4x+41}{(x-1)(x+4)}$

Question 15:

$\frac{-3}{x+2}- \frac{(-5)}{x+3}= \frac{-3(x+3)-(-5)(x+2)}{(x+2)(x+3)}$
$\frac{-3x-9+5x+10}{(x+2)(x+3)}= \frac{2x+1}{(x+2)(x+3)}$

Question 16:

$\frac{4}{x}+ \frac{5}{x}=-3$
$\frac{9}{x}=-3$
x=-3

Question 17:

$\frac{1}{3x-6}- \frac{5}{x-2}=12$
$\frac{(x-2)-5(3x-6)}{(3x-6)(x-2)} = \frac{x-2-15x+30}{(3x-6)(x-2)}= \frac{-14x+28}{(3x-6)(x-2)}$

Question 18

1. the width w of a rectangular swimming pool is x+4. the area a of the pool is 2x^3-29+12. what is

Mathematics

1. the width w of a rectangular swimming pool is x+4. the area a of the pool is 2x^3-29+12. what is an expression for the length of the pool? a. 2x^2+8x+3 b. 2x^2-8x-3 c. 2x^2-8x+3 d. 2x^2+8-3 2. simplify x/6x-x^2 a. 1/6-x; where x = 0,6 b. 1/6-x; where x=6 c. 1/6; where x=0 d. 1/6 3. simplify -12x4/x4+8x^5 a. -12/1+8x; where x= -1/8 b. -12/1+8x; where x= -1/8,0 4. simplify x+5/ x^2+6x+5 a. 1/x+1; where x= -1 b. 1/x+1; where x=-1, -5 5. simplify x^2-3x-18/x+3 a. x-3 b. x-6; where x= -3 c. x-6; where x= 6 d. 1/x+3; where x= -3 6. simplify 2/3a .

Step-by-step answer

P Answered by PhD

20

Question 1

To find the width of the rectangle, we divide the area by the length
$2x^{3}-29x+12$ ÷ x+4

We use the method of long division to get the answer. The method is shown in the first diagram below

$2x^{2}-8x+3$

Question 2:
$\frac{x}{6x-x^{2} } = \frac{x}{x(6-x)} = \frac{1}{6-x}$

Question 3:
$\frac{-12 x^{4} }{x^{4}+8 x^{5} }= \frac{-12 x^{4} }{ x^{4}(1+8x)}= \frac{-12}{1+8x}$

Question 4:
$\frac{x+5}{x^{2}+6x+5}= \frac{x+5}{(x+1)(x+5)}= \frac{1}{x+1}$

Question 5:
$\frac{x^{2}-3x-18} {x+3}= \frac{(x-6)(x+3)}{x+3}= \frac{x-6}{1}=x-6$

Question 6:
$\frac{2}{3a}$ × $\frac{2}{a^{2}}$ = $\frac{4}{3a^{3} }$ where $a \neq 0$

Question 7: (Question is not written well)
$\frac{x-5}{4x+8}$ × $(12x^{2}+32x+8)$
$\frac{12 x^{3}-28 x^{2} -152x-40 }{4x+8}$
By performing long division we get an answer $3 x^{2} -x-36$ with remainder of 248

Question 8:
$( \frac{x^{2}-16} {x-1})$ ÷ (x+4)

$( \frac{ x^{2}-16 }{x-1})$ × $\frac{1}{x+4}$
$\frac{(x+4)(x-1)}{x-1}$ × $\frac{1}{x+4}$
Cancelling out x+4

we obtain $\frac{x+1}{x-1}$

Question 9:
$\frac{x^{2}+2x+1} {x-2}$ ÷ $\frac{x^{2-1} }{x^{2}-4 }$
$\frac{ x^{2}+2x+1 }{x-2}$ × $\frac{x^{2}-4 }{x^{2}-1}$
Factorise all the quadratic expression gives
$\frac{(x+1)(x+1)}{x-2}$ × $\frac{(x-2)(x+2)}{(x+1)(x-1)}$
Cancelling out (x+1)

and

gives a simplest form
$\frac{(x+1)(x+2)}{x-1}$

Question 10:

$\frac{24 w^{10}+8w^{12} }{4 x^{4} }= \frac{24w^{10} }{4 x^{4} } + \frac{8 w^{12} }{4 x^{4} }$
Cancelling out the constants of each fraction
$\frac{6w^{10} }{x^{4} }+ \frac{2w^{12} }{x^{4}}= \frac{6w^{10}+2w^{12} }{ x^{4}}$

Question 11:

$\frac{-6m^{9}-6m^{8}-16m^{6} }{2m^{3} } = \frac{-2m^{6}(3m^{3}-3m^{2}-8)}{2m^{3} }$
Cancelling $2m^{3}$ gives us the simplified form
$-m^{3}(3m^{3}-3m^{2}-8) = -3m^{6}+3m^{5}+8m^{3}$

Question 12:

$\frac{-4x}{x+7} - \frac{8}{x-7} = \frac{-4x(x-7)-8(x+7)}{(x+7)(x-7)}$
$\frac{-4 x^{2} +28x-8x-56}{(x+7)(X-7)}= \frac{-4 x^{2} +20x-56}{(x+7)(x-7)}$
Factorising the numerator expression
$\frac{(-4x+28)(x-2)}{(x+7)(x-7)} = \frac{-4(x-7)(x-2)}{(x+7)(x-7)}$
Cancelling out x-7

gives the simplified form
$\frac{-4x+8}{x-7}$

Question 13:

$\frac{3}{x-3} - \frac{5}{x-2}= \frac{x3(x-2)-5(x-2)}{y(x-3)(x-2)}$
$\frac{3x-6-5x+15}{(x-3)(x-2)}= \frac{-2x+9}{(x-3)(x-2)}$

Question 14:

$\frac{9}{x-1}- \frac{5}{x+4}= \frac{9(x+4)-5(x-1)}{(x-1)(x+4)}$ $\frac{9x+36-5x+5}{(x-1)(x+4)}= \frac{4x+41}{(x-1)(x+4)}$

Question 15:

$\frac{-3}{x+2}- \frac{(-5)}{x+3}= \frac{-3(x+3)-(-5)(x+2)}{(x+2)(x+3)}$
$\frac{-3x-9+5x+10}{(x+2)(x+3)}= \frac{2x+1}{(x+2)(x+3)}$

Question 16:

$\frac{4}{x}+ \frac{5}{x}=-3$
$\frac{9}{x}=-3$
x=-3

Question 17:

$\frac{1}{3x-6}- \frac{5}{x-2}=12$
$\frac{(x-2)-5(3x-6)}{(3x-6)(x-2)} = \frac{x-2-15x+30}{(3x-6)(x-2)}= \frac{-14x+28}{(3x-6)(x-2)}$

Question 18

1. the width w of a rectangular swimming pool is x+4. the area a of the pool is 2x^3-29+12. what is

Mathematics

A simple random sample was taken of 44 water bottles from a bottling plant’s warehouse. The dissolvedoxygen content (in mg/L) was measured for each bottle, with the results below.11.53, 8.35, 11.66, 11.54, 9.83, 5.92, 7.14, 8.41, 8.99, 13.81, 10.53, 7.4, 6.7, 8.42, 8.4, 8.18, 9.5, 7.22, 9.87, 6.52, 8.55, 9.75, 9.27, 10.61, 8.89, 10.01, 11.17, 7.62, 6.43, 9.09, 8.53, 7.91, 8.13, 7.7, 10.45, 11.3, 10.98, 8.14, 11.48, 8.44, 12.52, 10.12, 8.09, 7.34 Here the sample mean is 9.14 mg/L and the sample standard deviation is 1.78 mg/L. The population standard

Step-by-step answer

P Answered by Specialist

a) $9.14-2.33\frac{2}{\sqrt{44}}=8.44$

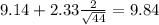
$9.14+2.33\frac{2}{\sqrt{44}}=9.84$

b) The 98% confidence interval would be given by (8.44;9.84)

For this case we can conclude that we have 98% of confidence that the true mean for the oxygen content is between 8.44 and 9.84 mg/L

Step-by-step explanation:

Previous concepts

A confidence interval is "a range of values that’s likely to include a population value with a certain degree of confidence. It is often expressed a % whereby a population means lies between an upper and lower interval".

The margin of error is the range of values below and above the sample statistic in a confidence interval.

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

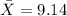$\bar X=9.14$ represent the sample mean for the sample

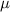$\mu$ population mean (variable of interest)

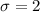$\sigma=2$ represent the population standard deviation

n=44 represent the sample size

Part a

The confidence interval for the mean is given by the following formula:

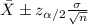$\bar X \pm z_{\alpha/2}\frac{\sigma}{\sqrt{n}}$ (1)

In order to calculate the critical value 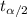$t_{\alpha/2}$ we need to find first the degrees of freedom, given by:

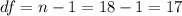
df=n-1=18-1=17

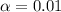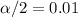Since the Confidence is 0.98 or 98%, the value of $\alpha=0.01$ and $\alpha/2 =0.01$ , and we can use excel, a calculator or a table to find the critical value. The excel command would be: "=-NORM.INV(0.01,0,1)".And we see that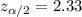 $z_{\alpha/2}=2.33$

Now we have everything in order to replace into formula (1):

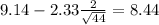
$9.14-2.33\frac{2}{\sqrt{44}}=8.44$

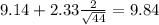
$9.14+2.33\frac{2}{\sqrt{44}}=9.84$

Part b

The 98% confidence interval would be given by (8.44;9.84)

For this case we can conclude that we have 98% of confidence that the true mean for the oxygen content is between 8.44 and 9.84 mg/L

A gas at 8.4 atm has a volume of 1.9 L. What volume would the gas have at 8.3 atm?

Step-by-step answer

Faq

Try asking the Studen AI a question.