StudenGPT : asked on queenskyyt

15.04.2021

Find the indefinite integral. (Remember to use absolute values where appropriate. Remember the constant of integration.) \[\int \frac{1}{10-6 x} d x\]

Step-by-step answer

s Studen AI

33 500 answers

4.9 rating

Unlock the full answer

1 students found this answer

helpful

To solve the integral \[ \int \frac{1}{10 - 6x} \, dx, \] we'll follow these steps: ### Step 1: Identify the Substitution The integrand $\frac{1}{10 - 6x}$ resembles the derivative of a function in its denominator. Hence, we can use a substitution. Let \[ u = 10 - 6x. \] ### Step 2: Differentiate the Substitution Now we need to find $du$: \[ du = -6 \, dx \quad \Rightarrow \quad dx = -\frac{1}{6} \, du. \] ### Step 3: Rewrite the Integral Now substituting $u$ and $dx$ into the integral gives: \[ \int \frac{1}{10 - 6x} \, dx = \int \frac{1}{u} \left(-\frac{1}{6}\right) du. \] ### Step 4: Factor Out Constants Factor out the constant $-\frac{1}{6}$: \[ -\frac{1}{6} \int \frac{1}{u} \, du. \] ### Step 5: Integrate The integral of $\frac{1}{u}$ is the natural logarithm: \[ -\frac{1}{6} \cdot \ln |u| + C, \] where $C$ is the constant of integration. ### Step 6: Substitute Back Now, substitute back $u = 10 - 6x$: \[ -\frac{1}{6} \ln |10 - 6x| + C. \] ### Final Result Thus, the indefinite integral is: \[ \int \frac{1}{10 - 6x} \, dx = -\frac{1}{6} \ln |10 - 6x| + C. \] ### Verification To verify our result, we can differentiate our final answer. The derivative of \[ -\frac{1}{6} \ln |10 - 6x| + C \] is computed as follows: Using the chain rule: \[ \frac{d}{dx} \left(-\frac{1}{6} \ln |10 - 6x|\right) = -\frac{1}{6} \cdot \frac{1}{10 - 6x} \cdot (-6) = \frac{1}{10 - 6x}. \] This confirms that our integral is correct, as differentiating our answer returns us to the original integrand. Therefore, the final answer is: \[ \int \frac{1}{10 - 6x} \, dx = -\frac{1}{6} \ln |10 - 6x| + C. \]

It is was helpful?

Helpful Useless

Faq

StudenGPT

Find the indefinite integral. (Remember to use absolute values where appropriate. Remember the constant of integration.)

Step-by-step answer

P Answered by Studen AI

To find the indefinite integral \[ \int \csc(8x) \, dx, \] we'll use a standard technique involving the identity of the cosecant function and integration techniques. Let's break down the steps: ### Step 1: Rewrite the integral The cosecant function is the reciprocal of the sine function: \[ \csc(8x) = \frac{1}{\sin(8x)}. \] Thus, we can rewrite the integral as: \[ \int \frac{1}{\sin(8x)} \, dx. \] ### Step 2: Use a substitution We can use the identity involving the cosecant function for integration. We will rewrite the integral in a more manageable form by multiplying and dividing by a suitable expression. One effective method is to multiply by $(\csc(8x) + \cot(8x))$. Therefore, our integral becomes: \[ \int \csc(8x) \, dx = \int \frac{\csc(8x)(\csc(8x) + \cot(8x))}{\csc(8x) + \cot(8x)} \, dx. \] This leads us to: \[ \int \frac{\csc^2(8x) + \csc(8x) \cot(8x)}{\csc(8x) + \cot(8x)} \, dx. \] ### Step 3: Substitute u for $\csc(8x) + \cot(8x)$ Let: \[ u = \csc(8x) + \cot(8x). \] To differentiate $u$ with respect to $x$, we use the derivatives: - The derivative of $\csc(8x)$ is given by $-8\csc(8x)\cot(8x)$. - The derivative of $\cot(8x)$ is given by $-8\csc^2(8x)$. Thus, the total derivative becomes: \[ \frac{du}{dx} = -8(\csc(8x)\cot(8x) + \csc^2(8x)). \] This allows us to express $dx$: \[ dx = \frac{du}{-8(\csc(8x)\cot(8x) + \csc^2(8x))}. \] ### Step 4: Substitute back into the integral Now our integral in $u$ can be represented as $ -\frac{1}{8}\int \frac{du}{u}$. The integral of $ \frac{1}{u} $ is: \[ \int \frac{1}{u} \, du = \ln |u| + C, \] where $C$ is the constant of integration. Substituting back $u$: \[ -\frac{1}{8} \ln |u| + C = -\frac{1}{8} \ln |\csc(8x) + \cot(8x)| + C. \] ### Step 5: Final expression Thus, the indefinite integral is: \[ \int \csc(8x) \, dx = -\frac{1}{8} \ln |\csc(8x) + \cot(8x)| + C. \] ### Step 6: Verification To verify our solution, we can differentiate our result: 1. Differentiate $ -\frac{1}{8} \ln |\csc(8x) + \cot(8x)| + C $, 2. Apply the chain rule and quotient rule as needed. The process confirms the original integrand, $ \csc(8x) $. Thus, the solution to the integral \[ \int \csc(8x) \, dx = -\frac{1}{8} \ln |\csc(8x) + \cot(8x)| + C, \] is correct.

Mathematics

1. Write the form of the partial fraction decomposition of the rational expression. Do not solve for the constants. 8x − 4/x(x2 + 1)2 2. Use partial fractions to find the indefinite integral. (Remember to use absolute values where appropriate. Use C for the constant of integration). 2x3 - 16x2 - 39x + 20/x2 - 8x - 20 x dx 3. Use partial fractions to find the indefinite integral. (Remember to use absolute values where appropriate. Use C for the constant of integration). x2/x4 - 42x2 - 343 x dx

Step-by-step answer

P Answered by Master

Step-by-step explanation:

To write the form of the partial fraction decomposition of the rational expression:

We have:

$\mathbf{\dfrac{8x-4}{x(x^2+1)^2}= \dfrac{A}{x}+\dfrac{Bx+C}{x^2+1}+\dfrac{Dx+E}{(x^2+1)^2}}$

Using partial fraction decomposition to find the definite integral of:

$\dfrac{2x^3-16x^2-39x+20}{x^2-8x-20}dx$

By using the long division method; we have:

$x^2-8x-20 | \dfrac{2x}{2x^3-16x^2-39x+20 }$

- 2x^3 -16x^2-40x

x+ 20

So;

$\dfrac{2x^3-16x^2-39x+20}{x^2-8x-20}= 2x+\dfrac{x+20}{x^2-8x-20}$

By using partial fraction decomposition:

$\dfrac{x+20}{(x-10)(x+2)}= \dfrac{A}{x-10}+\dfrac{B}{x+2}$

$= \dfrac{A(x+2)+B(x-10)}{(x-10)(x+2)}$

x + 20 = A(x + 2) + B(x - 10)

x + 20 = (A + B)x + (2A - 10B)

Now; we have to relate like terms on both sides; we have:

A + B = 1 ; 2A - 10 B = 20

By solvong the expressions above; we have:

$A = \dfrac{5}{2}$ $B = \dfrac{3}{2}$

Now;

$\dfrac{x+20}{(x-10)(x+2)} = \dfrac{5}{2(x-10)} + \dfrac{3}{2(x+2)}$

Thus;

$\dfrac{2x^3-16x^2-39x+20}{x^2-8x-20}= 2x + \dfrac{5}{2(x-10)}+ \dfrac{3}{2(x+2)}$

Now; the integral is:

$\int \dfrac{2x^3-16x^2-39x+20}{x^2-8x-20} \ dx = \int \begin {bmatrix} 2x + \dfrac{5}{2(x-10)}+ \dfrac{3}{2(x+2)} \end {bmatrix} \ dx$

$\mathbf{\int \dfrac{2x^3-16x^2-39x+20}{x^2-8x-20} \ dx = x^2 + \dfrac{5}{2}In | x-10|\dfrac{3}{2} In |x+2|+C}$

3. Due to the fact that the maximum words this text box can contain are 5000 words, we decided to write the solution for question 3 and upload it in an image format.

Please check to the attached image below for the solution to question number 3.

$1. Write the form of the partial fraction decomposition of the rational expression. Do not solve for$
$1. Write the form of the partial fraction decomposition of the rational expression. Do not solve for$
$1. Write the form of the partial fraction decomposition of the rational expression. Do not solve for$

Mathematics

Step-by-step answer

P Answered by Specialist

Step-by-step explanation:

To write the form of the partial fraction decomposition of the rational expression:

We have:

$\mathbf{\dfrac{8x-4}{x(x^2+1)^2}= \dfrac{A}{x}+\dfrac{Bx+C}{x^2+1}+\dfrac{Dx+E}{(x^2+1)^2}}$

Using partial fraction decomposition to find the definite integral of:

$\dfrac{2x^3-16x^2-39x+20}{x^2-8x-20}dx$

By using the long division method; we have:

$x^2-8x-20 | \dfrac{2x}{2x^3-16x^2-39x+20 }$

- 2x^3 -16x^2-40x

x+ 20

So;

$\dfrac{2x^3-16x^2-39x+20}{x^2-8x-20}= 2x+\dfrac{x+20}{x^2-8x-20}$

By using partial fraction decomposition:

$\dfrac{x+20}{(x-10)(x+2)}= \dfrac{A}{x-10}+\dfrac{B}{x+2}$

$= \dfrac{A(x+2)+B(x-10)}{(x-10)(x+2)}$

x + 20 = A(x + 2) + B(x - 10)

x + 20 = (A + B)x + (2A - 10B)

Now; we have to relate like terms on both sides; we have:

A + B = 1 ; 2A - 10 B = 20

By solvong the expressions above; we have:

$A = \dfrac{5}{2}$ $B = \dfrac{3}{2}$

Now;

$\dfrac{x+20}{(x-10)(x+2)} = \dfrac{5}{2(x-10)} + \dfrac{3}{2(x+2)}$

Thus;

$\dfrac{2x^3-16x^2-39x+20}{x^2-8x-20}= 2x + \dfrac{5}{2(x-10)}+ \dfrac{3}{2(x+2)}$

Now; the integral is:

$\int \dfrac{2x^3-16x^2-39x+20}{x^2-8x-20} \ dx = \int \begin {bmatrix} 2x + \dfrac{5}{2(x-10)}+ \dfrac{3}{2(x+2)} \end {bmatrix} \ dx$

$\mathbf{\int \dfrac{2x^3-16x^2-39x+20}{x^2-8x-20} \ dx = x^2 + \dfrac{5}{2}In | x-10|\dfrac{3}{2} In |x+2|+C}$

3. Due to the fact that the maximum words this text box can contain are 5000 words, we decided to write the solution for question 3 and upload it in an image format.

Please check to the attached image below for the solution to question number 3.

Mathematics

Evaluate the indefinite integral. (remember to use absolute values where appropriate. use c for the constant of integration.) dx hx + q (h ≠ 0

Step-by-step answer

P Answered by PhD

$\displaystyle \int {(hx + q)} \, dx = \frac{hx^2}{2} + qx + C$

General Formulas and Concepts:

Calculus

Integration

Integrals[Indefinite Integrals] Integration Constant C

Integration Rule [Reverse Power Rule]: $\displaystyle \int {x^n} \, dx = \frac{x^{n + 1}}{n + 1} + C$

Integration Property [Multiplied Constant]: $\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx$

Integration Property [Addition/Subtraction]: $\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx$

Step-by-step explanation:

*Note:

Assume h and q are arbitrary constants, where h and q ≠ 0.

Step 1: Define

Identify

$\displaystyle \int {(hx + q)} \, dx$

Step 2: Integrate

[Integral] Rewrite [Integration Property - Addition/Subtraction]: $\displaystyle \int {(hx + q)} \, dx = \int {hx} \, dx + \int {q} \, dx$ [Integrals] Rewrite [Integration Property - Multiplied Constant]: $\displaystyle \int {(hx + q)} \, dx = h\int {x} \, dx + q\int {} \, dx$ [Integrals] Reverse Power Rule: $\displaystyle \int {(hx + q)} \, dx = h \Big( \frac{x^2}{2} \Big) + qx + C$ Simplify: $\displaystyle \int {(hx + q)} \, dx = \frac{hx^2}{2} + qx + C$

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration

Mathematics

Evaluate the indefinite integral. (remember to use absolute values where appropriate. use c for the constant of integration.) dx hx + q (h ≠ 0

Step-by-step answer

P Answered by PhD

$\displaystyle \int {(hx + q)} \, dx = \frac{hx^2}{2} + qx + C$

General Formulas and Concepts:

Calculus

Integration

Integrals[Indefinite Integrals] Integration Constant C

Integration Rule [Reverse Power Rule]: $\displaystyle \int {x^n} \, dx = \frac{x^{n + 1}}{n + 1} + C$

Integration Property [Multiplied Constant]: $\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx$

Integration Property [Addition/Subtraction]: $\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx$

Step-by-step explanation:

*Note:

Assume h and q are arbitrary constants, where h and q ≠ 0.

Step 1: Define

Identify

$\displaystyle \int {(hx + q)} \, dx$

Step 2: Integrate

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration

Mathematics

Find the indefinite integral. (remember to use absolute values where appropriate. use c for the constant of integration.) x2 − 22x dx

Step-by-step answer

P Answered by PhD

$\displaystyle \int {(x^2 - 22x)} \, dx = \frac{x^3}{3} - 11x^2 + C$

General Formulas and Concepts:

Calculus

Integration

Integrals[Indefinite Integrals] Integration Constant C

Integration Rule [Reverse Power Rule]: $\displaystyle \int {x^n} \, dx = \frac{x^{n + 1}}{n + 1} + C$

Integration Property [Multiplied Constant]: $\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx$

Integration Property [Addition/Subtraction]: $\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx$

Step-by-step explanation:

Step 1: Define

Identify

$\displaystyle \int {(x^2 - 22x)} \, dx$

Step 2: Integrate

[Integral] Rewrite [Integration Property - Addition/Subtraction]: $\displaystyle \int {(x^2 - 22x)} \, dx = \int {x^2} \, dx - \int {22x} \, dx$ [2nd Integral] Rewrite [Integration Property - Multiplied Constant]: $\displaystyle \int {(x^2 - 22x)} \, dx = \int {x^2} \, dx - 22\int {x} \, dx$ [Integrals] Reverse Power Rule: $\displaystyle \int {(x^2 - 22x)} \, dx = \frac{x^3}{3} - 22 \Big( \frac{x^2}{2} \Big) + C$ Simplify: $\displaystyle \int {(x^2 - 22x)} \, dx = \frac{x^3}{3} - 11x^2 + C$

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration

Mathematics

Use partial fractions to find the indefinite integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) 1 /x^2 − 49 dx

Step-by-step answer

P Answered by PhD

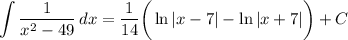
$\displaystyle \int {\frac{1}{x^2 - 49}} \, dx = \frac{1}{14} \bigg( \ln |x - 7| - \ln |x + 7| \bigg) + C$

General Formulas and Concepts:

Algebra I

Terms/Coefficients

Expanding/Factoring

Pre-Calculus

Partial Fraction Decomposition

Calculus

Differentiation

DerivativesDerivative Notation

Derivative Property [Addition/Subtraction]: $\displaystyle \frac{d}{dx}[f(x) + g(x)] = \frac{d}{dx}[f(x)] + \frac{d}{dx}[g(x)]$

Basic Power Rule:

f(x) = cxⁿf’(x) = c·nxⁿ⁻¹

Integration

Integrals[Indefinite Integrals] integration Constant C

Integration Property [Multiplied Constant]: 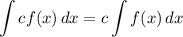$\displaystyle \int {cf(x)} \, dx = c \int {f(x)} \, dx$

Integration Property [Addition/Subtraction]: $\displaystyle \int {[f(x) \pm g(x)]} \, dx = \int {f(x)} \, dx \pm \int {g(x)} \, dx$

U-Substitution

Step-by-step explanation:

Step 1: Define

Identify

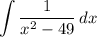
$\displaystyle \int {\frac{1}{x^2 - 49}} \, dx$

Step 2: Integrate Pt. 1

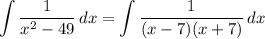
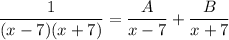
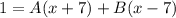
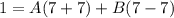
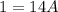
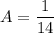
[Integrand] Factor: $\displaystyle \int {\frac{1}{x^2 - 49}} \, dx = \int {\frac{1}{(x - 7)(x + 7)}} \, dx$ [Integrand] Split [Partial Fraction Decomp]: $\displaystyle \frac{1}{(x - 7)(x + 7)} = \frac{A}{x - 7} + \frac{B}{x + 7}$ Rewrite: $\displaystyle 1 = A(x + 7) + B(x - 7)$ [Decomp] Substitute in x = 7: $\displaystyle 1 = A(7 + 7) + B(7 - 7)$ Simplify: $\displaystyle 1 = 14A$ Solve: $\displaystyle A = \frac{1}{14}$ [Decomp] Substitute in x = -7: $\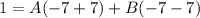displaystyle 1 = A(-7 + 7) + B(-7 - 7)$ Simplify: $\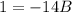displaystyle 1 = -14B$ Solve: $\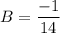displaystyle B = \frac{-1}{14}$ [Split Integrand] Substitute in variables: $\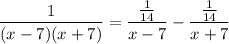displaystyle \frac{1}{(x - 7)(x + 7)} = \frac{\frac{1}{14}}{x - 7} - \frac{\frac{1}{14}}{x + 7}$

Step 3: Integrate Pt. 2

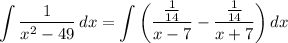
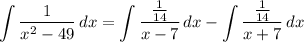
[Integral] Rewrite [Split Integrand]: $\displaystyle \int {\frac{1}{x^2 - 49}} \, dx = \int {\bigg( \frac{\frac{1}{14}}{x - 7} - \frac{\frac{1}{14}}{x + 7} \bigg)} \, dx$ [Integral] Rewrite [Integration Property - Addition/Subtraction]: $\displaystyle \int {\frac{1}{x^2 - 49}} \, dx = \int {\frac{\frac{1}{14}}{x - 7}} \, dx - \int {\frac{\frac{1}{14}}{x + 7}} \, dx$ [Integrals] Rewrite [Integration Property - Multiplied Constant]: $\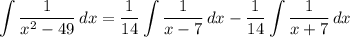displaystyle \int {\frac{1}{x^2 - 49}} \, dx = \frac{1}{14}\int {\frac{1}{x - 7}} \, dx - \frac{1}{14}\int {\frac{1}{x + 7}} \, dx$ Factor: $\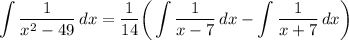displaystyle \int {\frac{1}{x^2 - 49}} \, dx = \frac{1}{14} \bigg( \int {\frac{1}{x - 7}} \, dx - \int {\frac{1}{x + 7}} \, dx \bigg)$

Step 4: Integrate Pt. 3

Identify variables for u-substitution.

Integral 1

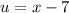
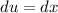
Set u: $\displaystyle u = x - 7$ [u] Differentiate [Basic Power Rule, Derivative Properties]: $\displaystyle du = dx$

Integral 2

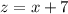
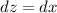
Set z: $\displaystyle z = x + 7$ [z] Differentiate [Basic Power Rule, Derivative Properties]: $\displaystyle dz = dx$

Step 5: Integrate Pt. 4

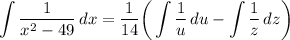
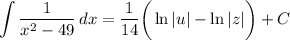
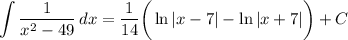
[Integrals] U-Substitution: $\displaystyle \int {\frac{1}{x^2 - 49}} \, dx = \frac{1}{14} \bigg( \int {\frac{1}{u}} \, du - \int {\frac{1}{z}} \, dz \bigg)$ [Integrals] Logarithmic Integration: $\displaystyle \int {\frac{1}{x^2 - 49}} \, dx = \frac{1}{14} \bigg( \ln |u| - \ln |z| \bigg) + C$ [Variables] Back-Substitute: $\displaystyle \int {\frac{1}{x^2 - 49}} \, dx = \frac{1}{14} \bigg( \ln |x - 7| - \ln |x + 7| \bigg) + C$

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Integration

Mathematics

Find the indefinite integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) 1 x 9x2 16 dx

Step-by-step answer

P Answered by Specialist

Expression given :

I = 9x^2+x+16

We know,

$\int {x^n} \, dx = \dfrac{x^{n+1}}{n+1} + c$

So,

$\int I dI = \int 9x^2.dx+\int x.dx + \int 16.dx\\\\= 9\int x^2.dx+\int x.dx + 16\int dx\\\\=9\times \dfrac{x^3}{3} + \dfrac{x^2}{2}+16x + c\\\\3x^3+\dfrac{x^2}{2}+16x + c$

Therefore, indefinite integration of given expression is $3x^3+\dfrac{x^2}{2}+16x + c$ .

Hence, this is the required solution.

Mathematics

Use partial fractions to find the indefinite integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) ∫x2/x1−20x2−125dx

Step-by-step answer

P Answered by PhD

125/6(In(x-25)) - 5/6(In(x+5))+C

Step-by-step explanation:

∫x2/x1−20x2−125dx

Should be

∫x²/(x²−20x−125)dx

First of all let's factorize the denominator.

x²−20x−125= x²+5x-25x-125

x²−20x−125= x(x+5) -25(x+5)

x²−20x−125= (x-25)(x+5)

∫x²/(x²−20x−125)dx= ∫x²/((x-25)(x+5))dx

x²/(x²−20x−125) =x²/((x-25)(x+5))

x²/((x-25)(x+5))= a/(x-25) +b/(x+5)

x²/= a(x+5) + b(x-25)

Let x=25

625 = a30

a= 625/30

a= 125/6

Let x= -5

25 = -30b

b= 25/-30

b= -5/6

x²/((x-25)(x+5))= 125/6(x-25) -5/6(x+5)

∫x²/(x²−20x−125)dx

=∫125/6(x-25) -∫5/6(x+5) Dx

= 125/6(In(x-25)) - 5/6(In(x+5))+C

StudenGPT

What is the grammatical name and function for the idea of profit and loss

Step-by-step answer

P Answered by Studen AI

The idea of profit and loss in grammar is known as a noun phrase. It functions as the subject or the object of a sentence, depending on the context.

In the sentence "Profit and loss are important concepts in business", the noun phrase "profit and loss" functions as the subject. It identifies what is important.

In the sentence "The company experienced significant profit and loss last year", the noun phrase "profit and loss" functions as the object. It receives the action of the verb "experienced" and specifies what the company experienced.

Noun phrases like "profit and loss" can be made up of multiple nouns or noun equivalents and can function in various ways within a sentence.

free Ask question

Today we have helped

2 084 students

just now

Mathematics

A fair coin is flipped three times. Let X be the number of heads observed. (a) Give both the possible values and probability mass function of X. (b) Find P(X ≥ 1) and P(X > 1). (c) Compute E[X] and V ar(X).

p Answered by PhD

just now

Mathematics

The diameter of the raw cookie is 2 1 2 inches. After baking the cookie, the diameter is 5 1 2 inches. By what factor does the cookie expand?

p Answered by PhD

1 minute ago