QUESTION 1)
The particle's equation of motion is
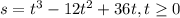
where s is measured in meters and t is in seconds.
The velocity at time,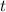 is given by the first derivative of the equation of motion of the particle.
is given by the first derivative of the equation of motion of the particle.
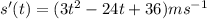
Question 1b).
To find the velocity after 3 seconds, we put 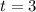 into the velocity function.
into the velocity function.


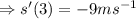
QUESTION 1C
To find the time that the particle is at rest, we equate the velocity (the first derivative formula) to zero and solve for t.
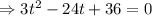
Divide through by 3 to get;
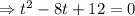
Factor:
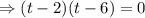
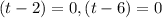
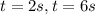
The particle is at rest when 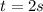 and
and 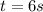 .
.
QUESTION 1d.
The particle is moving in a positive direction when the velocity is greater than zero.
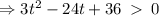
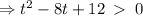
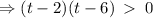
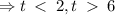
But 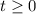 .
.
This implies that, the particle is moving in a positive direction on the interval,
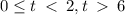
QUESTION 1e.
To find the total distance traveled after 8s, we substitute 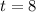 into the equation of motion of the particle.
into the equation of motion of the particle.
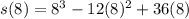
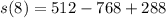
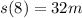
The particle covered 32m in the first 8 seconds.
QUESTION 1f
i) The acceleration at time 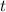 can be obtained by differentiating the velocity equation.
can be obtained by differentiating the velocity equation.
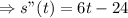
ii) To find the acceleration after 3 seconds, we substitute 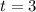 into the equation of acceleration.
into the equation of acceleration.
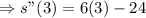
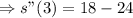
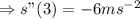
After 3 seconds, the particle is decelerating at 6 meters per seconds square.
QUESTION 2a
Given:
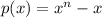
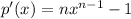
When 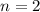 , then
, then
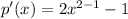
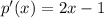
This implies that, p(x) is decreasing when
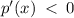
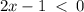
Therefore the function is decreasing on;
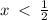
QUESTION 2b
When 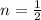
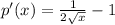
To find the interval over which the function is decreasing, we solve the inequality;
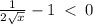
Therefore the function is decreasing on the interval;
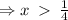
QUESTION 3a
The given parabola has equation
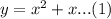
Let the two tangents from the external point; 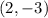 have equation;
have equation;
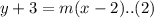
Put equation (1) into equation (2)
This implies that;
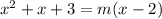
Rewrite to obtain a quadratic equation in  .
.
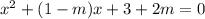
Since this is the point of intersection of a tangent and a parabola, the discriminant of this quadratic equation must be zero.
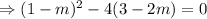
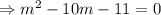
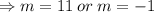
We substitute the values of m into equation (2) to obtain the equations of the two tangents to be;
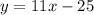 and
and 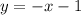
QUESTION 3b
Let the equation of the tangents from the external point (2,7) be
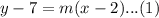
The given parabola has equation
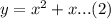
The discriminant of the intersection of these two equations yields;
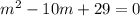
This quadratic equation has no real roots.
Hence there are no lines through the point (2,7) that are tangents to parabola.
We can see from the graph that this point is lying inside the parabola.
QUESTION 4
The given cubic function is
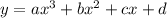
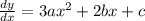
The horizontal tangents occurs when 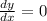 .
.
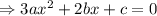
This occurs at (2,0).
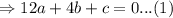
and (-2,6) .
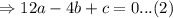
These points also lie on the curve so they must satisfy the equation of the curve;
Substituting (2,0) into the original equation gives;
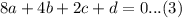
Substituting (-2,6) into the original equation gives;
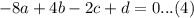
Solving the four equations simultaneously gives;
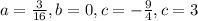
Hence the required cubic function;
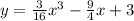
QUESTION 5a
Let
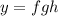
where 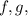 and
and 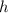 are differentiable.
are differentiable.
Using the product rule;
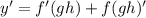
Use the product rule again;
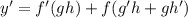
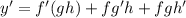 as required.
as required.